In problem “Convex Hull Algorithm” we have given a set of some points. The smallest polygon that can be formed with those points which contain all other points inside it will be called its convex hull.
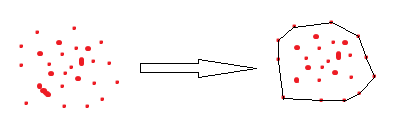
This can be achieved by using Jarvis Algorithm.
Table of Contents
Algorithm
- Initialize a leftmost point to 0.
- Declare a vector named result of Point type
- Traverse the points object array until the foremost left point is found
- Add that point to the result vector
- Find the next point “q” such that it is the most counterclockwise point off all other points
- Set p to point “q” for the next iteration.
- Keep adding up while “p” is not equal to leftmost.
Description
So our main idea to solve the convex hull is to use orientation. We are going to find and start with the leftmost or maybe the lowest X coordinate. And we can take it until all our points are found in which a set of some points can accumulate.
We are going to pass the Object array points of user class Point, which we already define it at the start of the code. Our arguments of points and lengths of the integer are passed into the convex hull function, where we will declare the vector named result in which we going to store our output.
Now initialize the leftmost point to 0. we are going to start it from 0, if we get the point which has the lowest x coordinate or the leftmost point we are going to change it.
Now traverse all the points and find out the lowest one. Store the position of leftmost to “p” and declare a point
Now, start a do-while loop in which the first thing we gonna does is adding up the first point as an output.
Now we have to find the most counterclockwise point to all other points, for this, we are going to use orientation. We made a separate function for this, which checks if the orientation of triplets is 2 or not if it is found to be 2 then update the value of point “q”.
This should be continued up until the “p” is not equal to leftmost.
Example
Given points are:
{ { 0, 3 }, { 2, 2 }, { 1, 1 }, { 2, 1 }, { 3, 0 }, { 0, 0 }, { 3, 3 } };
leftmost=0;
After traversing all the points, our first lowest x co-ordinate will be (0,3) it will store as a result.
Now it is going to check which x,y pair has most counterclockwise as it will give orientation as 2 and update the value of point “q”.
Pair to be found as (0,0).
Now, copy the value of point “q” into p as a next point for again finding out the most counterclockwise point.
Until the value of p is not equal to leftmost we are gonna use this loop.
Our output will be: (0,3), (0,0), (3,0), (3,3)
Implementation
C++ program for Convex Hull Algorithm
#include <iostream>
using namespace std;
#define INF 10000
struct Point
{
int x;
int y;
};
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
if (val == 0)
return 0;
return (val > 0) ? 1 : 2;
}
void convexHull(Point points[], int n)
{
if (n < 3)
return;
int next[n];
for (int i = 0; i < n; i++)
next[i] = -1;
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
int p = l, q;
do
{
q = (p + 1) % n;
for (int i = 0; i < n; i++)
if (orientation(points[p], points[i], points[q]) == 2)
q = i;
next[p] = q;
p = q;
}
while (p != l);
for (int i = 0; i < n; i++)
{
if (next[i] != -1)
cout << "(" << points[i].x << ", " << points[i].y << ")\n";
}
}
int main()
{
Point points[] = { { 0, 3 }, { 2, 2 }, { 1, 1 }, { 2, 1 }, { 3, 0 },
{ 0, 0 }, { 3, 3 } };
cout << "The points in the convex hull are: ";
int n = sizeof(points) / sizeof(points[0]);
convexHull(points, n);
return 0;
}The points in the convex hull are: (0, 3) (3, 0) (0, 0) (3, 3)
Java program for Convex Hull Algorithm
import java.util.*;
class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
}
class ConvexHull{
public static int OrientationMatch(Point check1, Point check2, Point check3) {
int val = (check2.y - check1.y) * (check3.x - check2.x) - (check2.x - check1.x) * (check3.y - check2.y);
if (val == 0)
return 0;
return (val > 0) ? 1 : 2;
}
public static void convex_hull(Point points[], int lengths) {
if (lengths<3) return;
Vector<Point> result = new Vector<Point> ();
int leftmost = 0;
for (int i = 1; i<lengths; i++)
if (points[i].x<points[leftmost].x)
leftmost = i;
int p = leftmost, pointq;
do {
result.add(points[p]);
pointq = (p + 1) % lengths;
for (int i = 0; i<lengths; i++) {
if (OrientationMatch(points[p], points[i], points[pointq]) == 2) {
pointq = i;
}
}
p = pointq;
}
while (p != leftmost);
System.out.print("The points in the convex hull are: ");
for (Point temp: result)
System.out.println("(" + temp.x + ", " + temp.y + ")");
}
public static void main(String[] args) {
Point points[] = new Point[7];
points[0] = new Point(0, 3);
points[1] = new Point(2, 3);
points[2] = new Point(1, 1);
points[3] = new Point(2, 1);
points[4] = new Point(3, 0);
points[5] = new Point(0, 0);
points[6] = new Point(3, 3);
int lengths = points.length;
convex_hull(points, lengths);
}
}
The points in the convex hull are: (0, 3) (0, 0) (3, 0) (3, 3)
Complexity Analysis for Convex Hull Algorithm
Time Complexity
O(m*n) where n is the number of input points and m is the number of output points.
Space Complexity
O(n) where n is the number of input points. Here we use an array of size N to find the next value.