In problem “Maximum Length of Repeated Subarray” we have given two arrays Array 1 and Array 2, your task is to find the maximum length of the sub-array that appears in both the arrays.
Table of Contents
Example
Input:
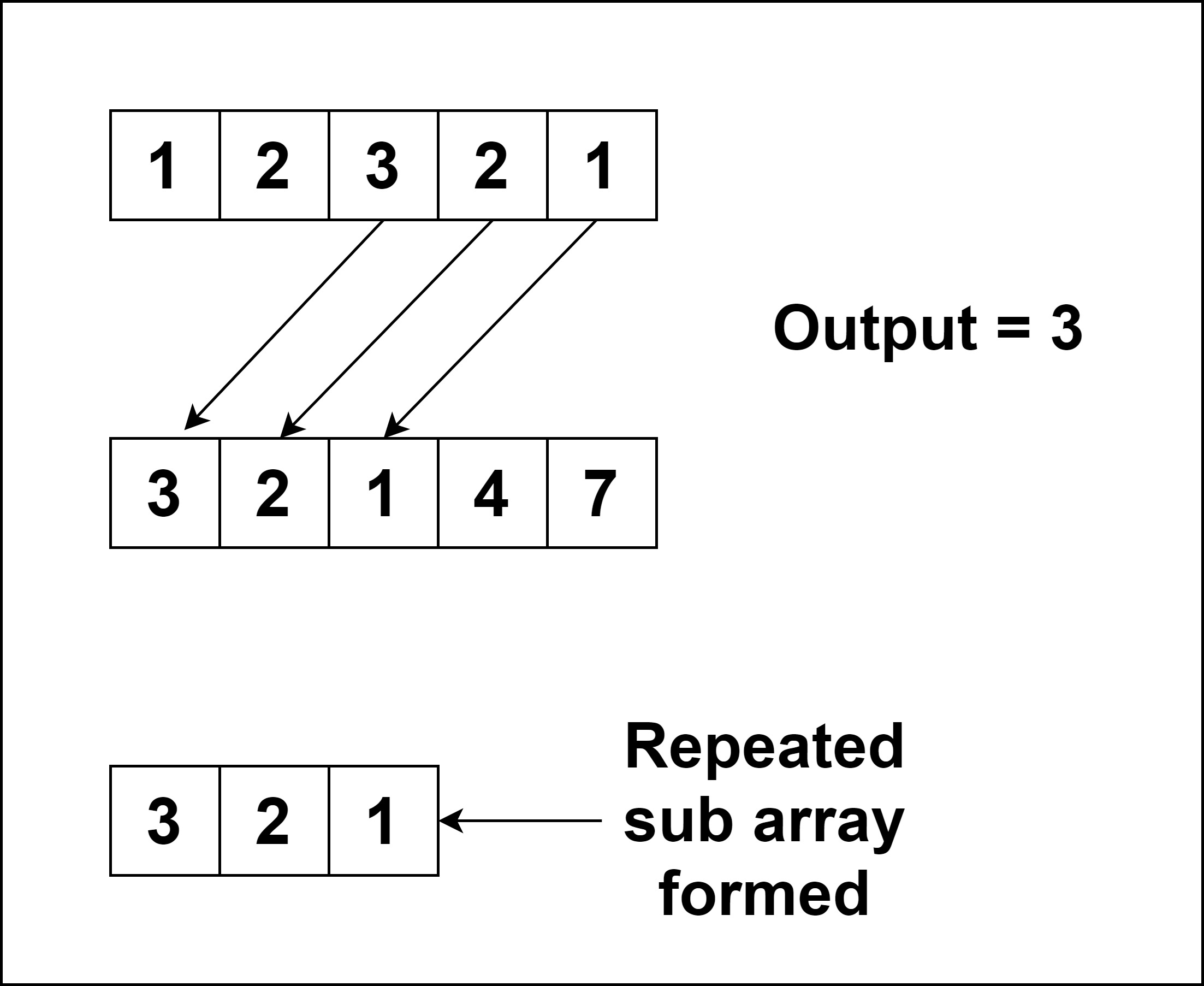
[1,2,3,2,1]
[3,2,1,4,7]
Output:
3
Explanation:
Because the maximum length of sub-array is 3 and the common array is [3,2,1]
Algorithm
- Set output to 0.
- Declare a variable integer array with a length 1 more than the length of the actual input array.
- Starting from the last index of array check if array1[i] is equal to array2[j] , if true then val[i][j]=val[i+1][j+1]+1.
- Check if output is less than val[i][j] then do output=val[i][j].
- Iterate over the whole array and check conditions we get the maximum output.
- Return output.
Explanation
To get our output, we need to do some simple traversing. For this, we are going to initialize the output to 0. Then we will declare the 2-D matrix of length one more than the length of array1 and array2.
We are going to traverse both the arrays from the last index of the array. So we will check some of the conditions and store the result in output.
So let us take an example and proceed further.
Example
Suppose are having an array as :
int array1[]={1,2,3,2,1};
int array2[]={3,2,1,4,7};
output=0;
- i=4, j=4;
if array1[i]==array2[j] returns false and is not gonna do anything.
output=0;
- i=4, j=3;
if array1[i]==array2[j] returns false and is not gonna do anything.
output=0;
- i=4, j=2;
if array1[i]==array2[j] returns true and val[i][j]=val[i+1][j+1]+1
then val[4][2]=val[5][3]+1=1 then val[i][j]=1.
then check if output < val[i][j] return true and do output=1.
output=1;
- i=4,j=1;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=4,j=0;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=3,j=4;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=3,j=3;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=3,j=2;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=3,j=1;
if array1[i]==array2[j] returns true and val[i][j]=val[i+1][j+1]+1
then val[3][1]= val[4][2] + 1 = 2 then val[3][1]=2.
then check if output < val[i][j] return true and do output=val[i][j].
output=2;
- i=3,j=0;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=2,j=4;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=2,j=3;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=2,j=2;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=2,j=1;
if array1[i]==array2[j] returns false and is not gonna do anything.
- i=2,j=0;
if array1[i]==array2[j] returns true and val[i][j]=val[i+1][j+1]+1
then val[2][0]= val[3][1] + 1 = 2 + 1 then val[2][0]=3.
then check if output < val[i][j] return true and do output=val[2][0].
output=3;
And this will be the maximum length of the repeated array that is 3 even after we find the elements equal in traversing but it won’t do updation in output, because that will not be the subarray
let say at i=1,j=1 we gonna find the next similar element so it will do val[1][1]=val[2][2]+1;
and if we check output < val[1][1] then every time it returns false and won’t do anything.
So here, the output is 3.
Implementation
C++ program for Maximum Length of Repeated Subarray
#include <iostream>
using namespace std;
int lengthOfRepeatedArray(int array1[], int array2[])
{
int output = 0;
int val[6][6]= {0};
for (int i = 4; i >= 0; --i)
{
for (int j = 4; j >= 0; --j)
{
if (array1[i] == array2[j])
{
val[i][j] = val[i+1][j+1] + 1;
if(output < val[i][j])
{
output = val[i][j];
}
}
}
}
return output;
}
int main()
{
int a[]= {1,2,3,2,1};
int b[]= {3,2,1,4,7};
cout<<lengthOfRepeatedArray(a,b);
return 0;
}
3
Java program for Maximum Length of Repeated Subarray
class repeatedArrayLength
{
public static int lengthOfRepeatedArray(int[] array1, int[] array2)
{
int output = 0;
int val[][] = new int[array1.length + 1][array2.length + 1];
for (int i = array1.length - 1; i >= 0; --i)
{
for (int j = array2.length - 1; j >= 0; --j)
{
if (array1[i] == array2[j])
{
val[i][j] = val[i+1][j+1] + 1;
if(output < val[i][j])
output = val[i][j];
}
}
}
return output;
}
public static void main(String []args)
{
int a[]= {1,2,3,2,1};
int b[]= {3,2,1,4,7};
System.out.println(lengthOfRepeatedArray(a,b));
}
}
3
Complexity Analysis for Maximum Length of Repeated Subarray
Time Complexity
O(a × b) where “a” is the size of the first array and “b” is the size of the second array.
Space Complexity
O(a × b) where “a” is the size of the first array and “b” is the size of the second array.