Table of Contents
Problem Statement
The problem “Boundary Traversal of binary tree” states that you are given a binary tree. Now you need to print the boundary view of a binary tree. Here boundary traversal means that all the nodes are shown as the boundary of the tree. The nodes are seen from the top side, left side, bottom side, and right side in an anti-clockwise direction. But if we would have printed all of these views directly that will result in the printing of the same nodes multiple times. So print the boundary view such that the nodes are not repeated.
Example
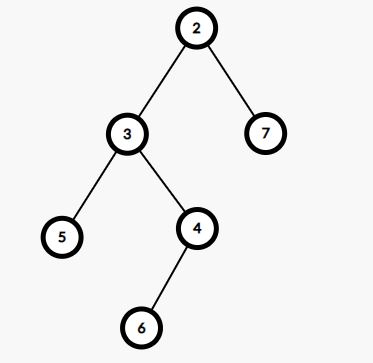
2 3 5 6 4 7
Explanation
Here, all nodes are boundary nodes. But we need to print the nodes in an anti-clockwise direction. Thus we start from the root that is 2. Then, we simply move in the same manner and print the nodes 2, 3, 4, 6, 4, 7.
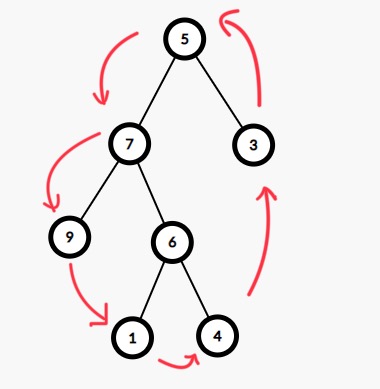
5 7 9 1 4 3
Approach
The problem asks us to print the boundary of the tree, here we have left, right, and bottom boundary. If the tree does not have any of the left or right boundary. the root itself is considered as the left or right boundary. There is also one condition that if we print the boundary nodes, we need to take care that none of the two nodes are printed multiple times.
To solve the problem, we will start with the left boundary of the tree. We say that a node belongs to the left boundary if that node is visible from the left side. Similarly, we define the right side nodes and leaf nodes. To print the left boundary, we will traverse the tree in such a way that if the root has a left node then move to that else move to its right node. Once we will get to the leaf node. We do not print the leaf nodes because we recursively print the leaf nodes separately. Once we are done with the left boundary.
We print the leaf nodes, by recursively first printing the left subtree leaves. After printing the left subtree leaves print the leaves in the right subtree. This way all leaf nodes will be printed in an anti-clockwise direction. Once we print the leaves, we print the nodes of the right boundary. This time the nodes need to be printed in a bottom-up manner. Thus inside the recursion, first we solve the left or right subtree of the tree and then pMicrrint the current node.
C++ code to print the Boundary Traversal of binary tree
#include<bits/stdc++.h>
using namespace std;
struct node {
int data;
node *left, *right;
};
// print the leaves (nodes from the bottom)
void printLeaves(node* root)
{
if(root){
// recursively solve the problem for the left subtree
printLeaves(root->left);
// if current node is a leaf
if ((root->left) == NULL && (root->right) == NULL)
cout<<root->data<<" ";
// recursively solve the problem for right subtree
printLeaves(root->right);
}
}
// print all the nodes of left boundary
// this function will not print the leaves viewed from left side
void printLeft(node* root)
{
if(root){
if(root->left != NULL){
cout<<root->data<<" ";
// recursively move down the left subtree
printLeft(root->left);
}
else if(root->right){
cout<<root->data<<" ";
// recursively move down the right subtree
printLeft(root->right);
}
}
}
// print all the nodes of right boundary
// this function will not print the leaves viewed from the right side
void printRight(node* root)
{
// printing is done after moving down the tree
// thus printing is done in bottom up manner
if(root){
if (root->right) {
printRight(root->right);
cout<<root->data<<" ";
}
else if (root->left) {
printRight(root->left);
cout<<root->data<<" ";
}
}
}
void boundaryUtil(node* root)
{
// first print the root, then print the left boundary
// then the leaves which are seen from bottom
// at last print the right boundary
if(root){
cout<<root->data<<" ";
printLeft(root->left);
printLeaves(root->left);
printLeaves(root->right);
printRight(root->right);
}
}
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
int main()
{
node* root = create(5);
root->left = create(7);
root->right = create(3);
root->left->left = create(9);
root->left->right = create(6);
root->left->right->left = create(1);
root->left->right->right = create(4);
boundaryUtil(root);
}
5 7 9 1 4 3
Java code to print Boundary Traversal of binary tree
import java.util.*;
class node{
int data;
node left, right;
}
class Main{
// print the leaves (nodes from the bottom)
static void printLeaves(node root)
{
if(root != null){
// recursively solve the problem for the left subtree
printLeaves(root.left);
// if current node is a leaf
if ((root.left) == null && (root.right) == null)
System.out.print(root.data+" ");
// recursively solve the problem for right subtree
printLeaves(root.right);
}
}
// print all the nodes of left boundary
// this function will not print the leaves viewed from left side
static void printLeft(node root)
{
if(root != null){
if(root.left != null){
System.out.print(root.data+" ");
// recursively move down the left subtree
printLeft(root.left);
}
else if(root.right != null){
System.out.print(root.data+" ");
// recursively move down the right subtree
printLeft(root.right);
}
}
}
// print all the nodes of right boundary
// this function will not print the leaves viewed from the right side
static void printRight(node root)
{
// printing is done after moving down the tree
// thus printing is done in bottom up manner
if(root != null){
if(root.right != null){
printRight(root.right);
System.out.print(root.data+" ");
}
else if(root.left != null){
printRight(root.left);
System.out.print(root.data+" ");
}
}
}
static void boundaryUtil(node root)
{
// first print the root, then print the left boundary
// then the leaves which are seen from bottom
// at last print the right boundary
if(root != null){
System.out.print(root.data+" ");
printLeft(root.left);
printLeaves(root.left);
printLeaves(root.right);
printRight(root.right);
}
}
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = tmp.right = null;
return tmp;
}
public static void main(String[] args){
node root = create(5);
root.left = create(7);
root.right = create(3);
root.left.left = create(9);
root.left.right = create(6);
root.left.right.left = create(1);
root.left.right.right = create(4);
boundaryUtil(root);
}
}5 7 9 1 4 3
Complexity Analysis
Time Complexity
O(N), because we have traversed through all of the nodes of the tree. We traverse through the nodes when we use printLeft, printRight, and printLeaves function. Thus the time complexity is linear.
Space Complexity
O(H), where H is the height of the tree. This is because the compiler stack uses space. And the functions used to print the boundary elements use recursion which counts for compiler stack.