Table of Contents
Problem Statement
The problem “Find distance between two nodes of a Binary Tree” states that you are given a binary tree and you are given two nodes. Now you need to find the minimum distance between these two nodes.
Example
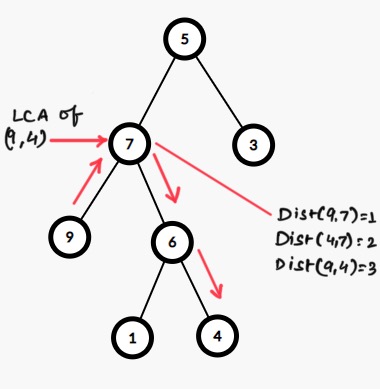
// Tree is shown using the image above node 1 = 9 node 2 = 4
3
Approach to find distance between two nodes of a Binary Tree
The problem asks to find distance between two nodes of a Binary Tree. So we will be given two nodes and a binary tree and two nodes. Now we need to find the minimum distance between these two nodes. This is a classical problem on binary trees, and generally in an n-ary tree. we solve the problem using the Least Common Ancestor of the tree. The Least Common Ancestor or LCA is the node which is at the least distance from both the nodes and lie on the path from these nodes to the root of the tree. But how does this LCA helps us to calculate the minimum distance?
The path of minimum distance always passes through the LCA of the two nodes. So, if somehow we know the distance of both nodes from the root and distance of their LCA from the root. We can compute a simple formula to find the minimum distance. We will add the distance of both nodes from the root then subtract twice the distance of their LCA from the root of the tree. So in the
Code
C++ code to print Bottom View of a Binary Tree
#include<bits/stdc++.h>
using namespace std;
struct node {
int data;
node *left, *right;
};
node* create(int data){
node* tmp = new node();
tmp->data = data;
tmp->left = tmp->right = NULL;
return tmp;
}
// calculates distance for the node from the root
int findDistUtil(node* root, int n, int lev){
if(!root)
return -1;
if(root->data == n)
return lev;
else{
int left = findDistUtil(root->left, n, lev+1);
int right = findDistUtil(root->right, n, lev+1);
return (left != -1) ? left : right;
}
}
node* findLCA(node* root, int n1, int n2){
if(!root)
return NULL;
if(root->data == n1 || root->data == n2){
return root;
} else {
// check if leftSubTree has n1 or n2 or both
node* leftSubTree = findLCA(root->left, n1, n2);
// check if rightSubTree has n1 or n2 or both
node* rightSubTree = findLCA(root->right, n1, n2);
if(leftSubTree && rightSubTree)
return root;
// if we don't find one nodes in left and one node in right subtree
// then the lca must be either in left subtree or right subtree
return (leftSubTree != NULL) ? leftSubTree : rightSubTree;
}
}
int computeMinDistance(node* root, int n1, int n2){
node* lca = findLCA(root, n1, n2);
int n1dist = findDistUtil(root, n1, 0);
int n2dist = findDistUtil(root, n2, 0);
int lcadist = findDistUtil(root, lca->data, 0);
return n1dist + n2dist - 2*lcadist;
}
int main()
{
node* root = create(5);
root->left = create(7);
root->right = create(3);
root->left->left = create(9);
root->left->right = create(6);
root->left->right->left = create(1);
root->left->right->right = create(4);
cout<<computeMinDistance(root, 9, 4);
}
3
Java code to print Bottom View of a Binary Tree
import java.util.*;
class node{
int data;
node left, right;
}
class Main{
static node create(int data){
node tmp = new node();
tmp.data = data;
tmp.left = tmp.right = null;
return tmp;
}
// calculates distance for the node from the root
static int findDistUtil(node root, int n, int lev){
if(root == null)
return -1;
if(root.data == n)
return lev;
else{
int left = findDistUtil(root.left, n, lev+1);
int right = findDistUtil(root.right, n, lev+1);
return (left != -1) ? left : right;
}
}
static node findLCA(node root, int n1, int n2){
if(root == null)
return null;
if(root.data == n1 || root.data == n2){
return root;
} else {
// check if leftSubTree has n1 or n2 or both
node leftSubTree = findLCA(root.left, n1, n2);
// check if rightSubTree has n1 or n2 or both
node rightSubTree = findLCA(root.right, n1, n2);
if(leftSubTree != null && rightSubTree != null)
return root;
// if we don't find one nodes in left and one node in right subtree
// then the lca must be either in left subtree or right subtree
return (leftSubTree != null) ? leftSubTree : rightSubTree;
}
}
static int computeMinDistance(node root, int n1, int n2){
node lca = findLCA(root, n1, n2);
int n1dist = findDistUtil(root, n1, 0);
int n2dist = findDistUtil(root, n2, 0);
int lcadist = findDistUtil(root, lca.data, 0);
return n1dist + n2dist - 2*lcadist;
}
public static void main(String[] args)
{
node root = create(5);
root.left = create(7);
root.right = create(3);
root.left.left = create(9);
root.left.right = create(6);
root.left.right.left = create(1);
root.left.right.right = create(4);
System.out.print(computeMinDistance(root, 9, 4));
}
}3
Complexity Analysis
Time Complexity
O(N), even though the tree is being traversed multiple times. But that does not constitute polynomial time complexity. One of the operations is to find LCA of two nodes which is being done in O(N) time. Then we are finding the distance of nodes from root which is again done in O(1) time. This makes the problem “Find distance between two nodes of a Binary Tree” linear in terms of time complexity.
Space Complexity
O(H), this space is required for the compiler stack. Because all the functions are recursive functions which will make use of recursive stack.