Table of Contents
Problem Statement
The problem “Find postorder traversal of BST from preorder traversal” states that you are given preorder traversal of a binary search tree. Then using the given input find the postorder traversal.
Example
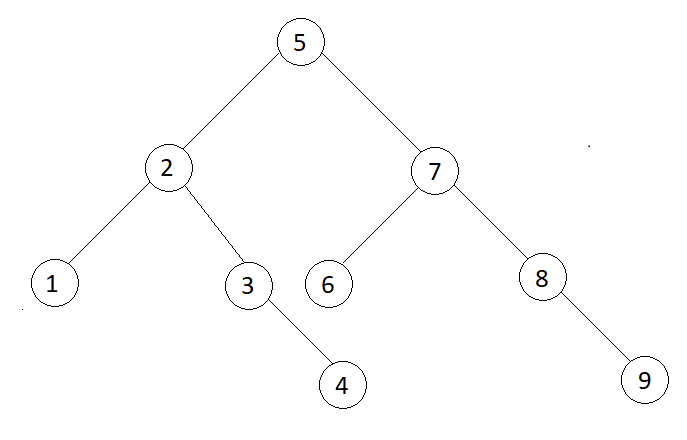
preorder traversal sequence: 5 2 1 3 4 7 6 8 9
1 4 3 2 6 9 8 7 5
Approach
The given problem says that we are provided with a preorder traversal sequence of a binary search tree. Now we are required to find the postorder traversal of the tree which has the same preorder traversal as input. We are required to solve this problem efficiently.
A naive approach is to first use the preorder traversal and build the BST. Then simply do a postorder traversal over this newly constructed tree. But this approach is inefficient regarding space. Because the constructed tree is acting as an overhead.
To solve the problem efficiently, we go through the input array. The input array is our preorder traversal. So we go through the preorder traversal and find whether the current element should lie. When we start with the first element we set a range from minimum integer value to maximum integer value. Because the preorder traversal has the root before the left and right subtree. We know that if the left subtree exists then elements should lie from a minimum integer value to a value lesser than the root. Similarly for the right subtree that should lie from the value of greater root to a maximum integer value. Now if the current element does not lie in this range. Then that should lie in the other subtree(that is if it does not lie in range for left subtree than it should lie in the right subtree and vice-versa).
Code
C++ code to find postorder traversal of BST from preorder traversal
#include<bits/stdc++.h>
using namespace std;
void preToPost(int input[], int n, int mn, int mx, int& idx)
{
// base case
if (idx == n)
return;
// if current element does not belong to current subtree
if (input[idx] < mn || input[idx] > mx) {
return;
}
// store the value of root ro print after printing its subtrees
int root = input[idx];
idx++;
// recursively solve for left and right subtree
preToPost(input, n, mn, root, idx);
preToPost(input, n, root, mx, idx);
// print root
cout<<root<<" ";
}
int main()
{
int input[] = {5, 2, 1, 3, 4, 7, 6, 8, 9};
int n = (sizeof input)/(sizeof input[0]);
int idx = 0;
preToPost(input, n, INT_MIN, INT_MAX, idx);
}
1 4 3 2 6 9 8 7 5
Java code to find postorder traversal of BST from preorder traversal
import java.util.*;
class Main{
static int idx = 0;
static void preToPost(int input[], int n, int mn, int mx)
{
// base case
if (idx == n)
return;
// if current element does not belong to current subtree
if (input[idx] < mn || input[idx] > mx) {
return;
}
// store the value of root ro print after printing its subtrees
int root = input[idx];
idx++;
// recursively solve for left and right subtree
preToPost(input, n, mn, root);
preToPost(input, n, root, mx);
// print root
System.out.print(root+" ");
}
public static void main(String[] args)
{
int input[] = {5, 2, 1, 3, 4, 7, 6, 8, 9};
int n = input.length;
preToPost(input, n, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
}1 4 3 2 6 9 8 7 5
Complexity Analysis
Time Complexity
O(N), because we have to traverse the whole of the given array.
Space Complexity
O(N), because of compiler stack which is being used for the recursive functions.