In “Iterative Inorder Traversal of a Binary Tree” problem we are given a binary tree. We need to traverse it in inorder fashion “iteratively”, without the recursion.
Table of Contents
Example
2
/ \
1 3
/ \
4 5
4 1 5 2 3
1
/ \
2 3
/ \
4 6
\
7
4 2 1 3 6 7
Algorithm
- Initialize a variable “curNode” as the root of the binary tree
- Initialize an empty stack, containing the nodes as they are traversed
- Do the following until either the stack is not empty or curNode has not become NULL:
- While curNode is not NULL:
- Push curNode into the stack
- Keep going to the leftmost child by changing the current node as curNode = curNode->left
- Now, the top node in the stack is the leftmost node of the current subtree, so we print the value of the top node in the stack
- Assign curNode as the right child of the top node in the stack as curNode = stack.top()->right
- Keep going to the leftmost child by changing the current node as curNode = curNode->left to process right subtree of this leftmost node
- Pop an element out of the stack
- While curNode is not NULL:
Explanation
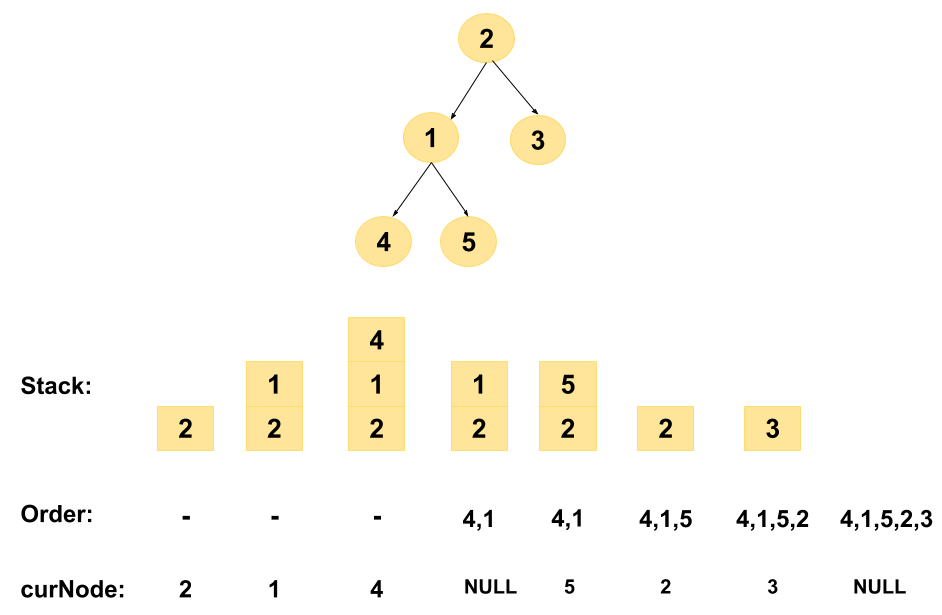
The program uses the idea the stack pops out the most recent element added, In the algorithm explained above, we simply infer that if the current node (which is initially the root of the tree) has a left child, then we keep pushing its left child into the stack until no more left children remain.
When the case arises such that the current node doesn’t have a left child, it’s clear that the top node in the stack is the “most recently leftmost node” added. So, it should come first in the remaining order of traversal. So, we start printing/adding it to our order list and pop it out of the stack. Once done, we are now clear about the fact that in the Left-curNode-Right (the inorder sequence), Left and Node part are traversed. So, the node’s right subtree is into the process!
Intuitively, since we want to apply the same process to the right subtree of the current node, we can generalize it as: curNode = curNode->right.
Implementation
C++ Program of Iterative Inorder Traversal of a Binary Tree
#include <bits/stdc++.h>
using namespace std;
struct treeNode
{
int value;
treeNode *left , *right;
treeNode(int x)
{
value = x;
left = NULL;
right = NULL;
}
};
void iterativeInorder(treeNode* root)
{
stack <treeNode*> ;
treeNode* curNode = root;elements
while(curNode != NULL || !elements.empty())
{
while(curNode != NULL)
{
elements.push(curNode);
curNode = curNode->left;
}
cout << elements.top()->value << " ";
curNode = elements.top()->right;
elements.pop();
}
}
int main()
{
treeNode* root = new treeNode(2);
root->left = new treeNode(1);
root->right = new treeNode(3);
root->left->left = new treeNode(4);
root->left->right = new treeNode(5);
iterativeInorder(root);
cout << endl;
return 0;
}
4 1 5 2 3
Java Program of Iterative Inorder Traversal of a Binary Tree
import java.util.Stack;
class treeNode
{
int value;
treeNode left, right;
public treeNode(int x)
{
value= x;
left = right = null;
}
}
class Tree
{
treeNode root;
void iterativeInorder()
{
Stack<treeNode> elements = new Stack<treeNode>();
treeNode curNode = root;
while (curNode != null || !elements.empty())
{
while (curNode != null)
{
elements.push(curNode);
curNode = curNode.left;
}
curNode = elements.peek().right;
System.out.print(elements.peek().value + " ");
elements.pop();
}
}
public static void main(String args[])
{
Tree tree = new Tree();
tree.root = new treeNode(2);
tree.root.left = new treeNode(1);
tree.root.left.left = new treeNode(4);
tree.root.left.right = new treeNode(5);
tree.root.right = new treeNode(3);
tree.iterativeInorder();
}
}4 1 5 2 3
Complexity Analysis
Time Complexity of Iterative Inorder Traversal of a Binary Tree
The time complexity is O(N), as we visit each node exactly once. Here, N is the number of nodes in the binary tree.
Space Complexity of Iterative Inorder Traversal of a Binary Tree
The space complexity is O(N). Considering the worst case, where the tree can be a skewed one, space complexity will be equal to the number of nodes in the binary tree.