Morris traversal is a method to traverse the nodes in a binary tree without using stack and recursion. Thus reducing the space complexity to linear.
Table of Contents
Inorder Traversal
Example
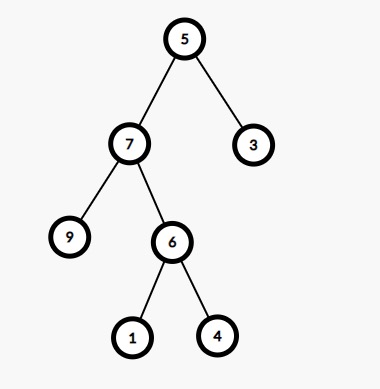
9 7 1 6 4 5 3
1 / \ 2 3 / \ 4 5
4 2 5 1 3
7 / \ 14 21
14 7 21
Algorithm
- Initialize a class Node which contains variables and pointers related to a node.
- Create a function MorrisTraversal which accepts the root node.
- If the root is null, return.
- Set reference curr as root. Traverse while curr is not null.
- If the left child of curr is null print value stored in curr and update curr as it’s a right child.
- Else update curr as a right node of the rightmost node of its left subtree and update curr as the left child of curr.
Code
C++ Program to traverse a binary tree using Morris Traversal
#include <bits/stdc++.h>
using namespace std;
struct Node{
int data;
struct Node* left;
struct Node* right;
};
void MorrisTraversal(struct Node* root){
struct Node *curr, *pre;
if(root == NULL)
return;
curr = root;
while(curr != NULL){
if(curr->left == NULL){
printf("%d ", curr->data);
curr = curr->right;
}
else{
pre = curr->left;
while (pre->right != NULL && pre->right != curr)
pre = pre->right;
if(pre->right == NULL) {
pre->right = curr;
curr = curr->left;
}
else{
pre->right = NULL;
cout<<curr->data<<" ";
curr = curr->right;
}
}
}
}
struct Node* newNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main(){
struct Node *root = newNode(5);
root->left = newNode(7);
root->right = newNode(3);
root->left->left = newNode(9);
root->left->right = newNode(6);
root->left->right->left = newNode(1);
root->left->right->right = newNode(4);
MorrisTraversal(root);
return 0;
}9 7 1 6 4 5 3
Java Program to traverse a binary tree using Morris Traversal
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BTree{
Node root;
void MorrisTraversal(Node root){
Node curr, pre;
if(root == null)
return;
curr = root;
while(curr != null){
if(curr.left == null){
System.out.print(curr.data + " ");
curr = curr.right;
}
else{
pre = curr.left;
while(pre.right != null && pre.right != curr)
pre = pre.right;
if(pre.right == null){
pre.right = curr;
curr = curr.left;
}
else{
pre.right = null;
System.out.print(curr.data + " ");
curr = curr.right;
}
}
}
}
public static void main(String args[]){
BTree tree = new BTree();
tree.root = new Node(5);
tree.root.left = new Node(7);
tree.root.right = new Node(3);
tree.root.left.left = new Node(9);
tree.root.left.right = new Node(6);
tree.root.left.right.left = new Node(1);
tree.root.left.right.right = new Node(4);
tree.MorrisTraversal(tree.root);
}
}9 7 1 6 4 5 3
Complexity Analysis
Time Complexity
O(N), because we traverse all the nodes in the binary tree. Since there are N nodes the time complexity is linear.
Space Complexity
O(1), because we are not using recursion or a stack to solve the problem. We have used a constant number of variables that account for constant space complexity.
Preorder Traversal
Example
1 / \ 2 3 / \ 4 5
1 2 4 5 3
7 / \ 14 21
7 14 21
Algorithm
- Initialize a class Node which contains variables and pointers related to a node.
- Create a function MorrisTraversal which accept node.
- Traverse while the node is not null.
- If the left child of a node is null print value stored in node and update node as it’s a right child.
- Else store left child of a node in another Node type variable curr.
- Traverse while the right child of curr is not null or not equal to the node and update curr as it’s a right child.
- If the right child of curr is null or equal to the node, update the right child of curr as null and node as it’s a right child.
- Else print node data and update the right child of curr as node and node as it’s a left child.
Code
C++ Program to traverse a binary tree using Morris Traversal
#include <bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node *left, *right;
};
node* newNode(int data){
node* temp = new node();
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void MorrisTraversal(node* root){
while(root){
if(root->left == NULL){
cout<<root->data<<" ";
root = root->right;
}
else{
node* curr = root->left;
while(curr->right && curr->right != root)
curr = curr->right;
if(curr->right == root){
curr->right = NULL;
root = root->right;
}
else{
cout<<root->data<<" ";
curr->right = root;
root = root->left;
}
}
}
}
int main(){
node *root = newNode(5);
root->left = newNode(7);
root->right = newNode(3);
root->left->left = newNode(9);
root->left->right = newNode(6);
root->left->right->left = newNode(1);
root->left->right->right = newNode(4);
MorrisTraversal(root);
return 0;
}5 7 9 6 1 4 3
Java Program to traverse a binary tree using Morris Traversal
class Node{
int data;
Node left, right;
Node(int item){
data = item;
left = right = null;
}
}
class BTree{
Node root;
void MorrisTraversal(){
MorrisTraversal(root);
}
void MorrisTraversal(Node node) {
while(node != null){
if(node.left == null) {
System.out.print(node.data + " ");
node = node.right;
}
else{
Node curr = node.left;
while (curr.right != null && curr.right != node) {
curr = curr.right;
}
if(curr.right == node){
curr.right = null;
node = node.right;
}
else{
System.out.print(node.data + " ");
curr.right = node;
node = node.left;
}
}
}
}
public static void main(String args[]){
BTree tree = new BTree();
tree.root = new Node(5);
tree.root.left = new Node(7);
tree.root.right = new Node(3);
tree.root.left.left = new Node(9);
tree.root.left.right = new Node(6);
tree.root.left.right.left = new Node(1);
tree.root.left.right.right = new Node(4);
tree.MorrisTraversal();
}
}
5 7 9 6 1 4 3
Complexity Analysis
Time Complexity
O(N), because we traverse all the nodes in the binary tree. Since there are N nodes the time complexity is linear.
Space Complexity
O(1), because we are not using recursion or a stack to solve the problem. We have used a constant number of variables that account for constant space complexity.