Table of Contents
Problem Statement
The problem “Maximum path sum in a triangle” states that you are given some integers. These integers are arranged in the form of a triangle. You are starting from the top of the triangle and need to reach the bottom row. For doing this, you move to the adjacent cells in the next row. So when you are moving down the triangle in the defined manner, what is the maximum sum you can achieve?
Example
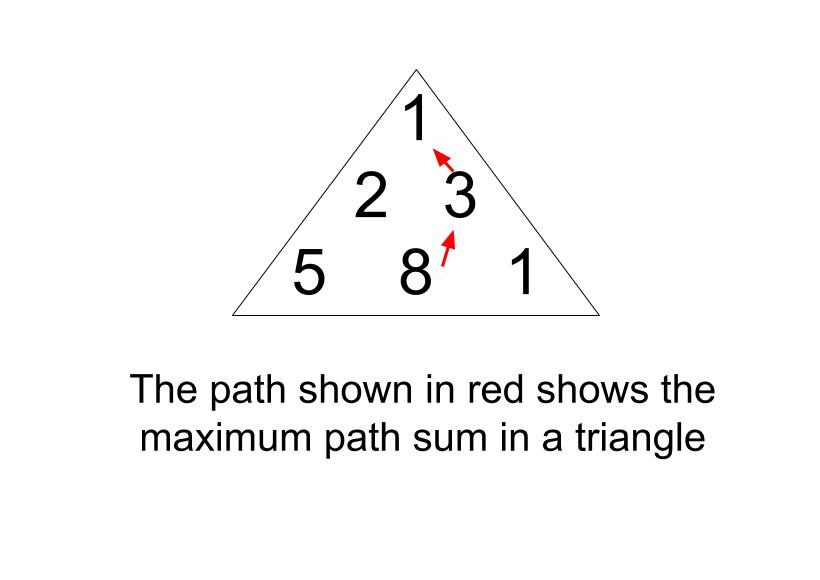
1 2 3 5 8 1
12
Explanation
You can simply move down the path in the following manner. 1-> 3-> 8, this path will make you attain a maximum sum that is 12.
Approach
So how do we solve the Maximum path sum in a triangle? Until now, we are pretty much familiar with these kinds of problems. Whenever we are provided with these kinds of problems. The brute force approach always is to first generate all the possible ways to reach your destination. And then keep on updating the answer for the optimal result, by calculating the sum for each path. But this approach is highly inefficient as this approach requires us to generate the paths. And we know that path generation is a task that has exponential time complexity which is not good.
So, to solve this we need to think of another approach. Then dynamic programming comes to our rescue. Because instead of generating the paths, if we could know somehow that what is the maximum that can be achieved from a cell to reach the bottom row. That way we can get the result for the cell which is adjacent to it but in the row above it. So, we use DP to solve the smaller subproblems. Then combining the results for those subproblems we find answers for the original problem.
First, we fill the answer for the cells in the last row. We know that the maximum sum that can be achieved if we start from the cells at the bottom row is the number itself. After that, we move to the row above the bottom row. For each cell in the current row, we can choose the DP values of the cells which are adjacent to it in the row just below it. This way we keep on going in an upward direction. As we reach the top row, we are done with the problem.
C++ code to find Maximum path sum in a triangle
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int maximumPathSumInTriangle(vector<vector<int>> &input)
{
int n = input.size();
// start from row above bottom row
// since the bottom row cells are the answers themselves
for(int i=n-2;i>=0;i--)
{
// start from left to right in column
for(int j=0;j<=i;j++)
{
if(input[i+1][j] > input[i+1][j+1])
input[i][j] += input[i+1][j];
else
input[i][j] += input[i+1][j+1];
}
}
return input[0][0];
}
int main()
{
int n;cin>>n; // number of rows
vector<vector<int>> input(n, vector<int>(n, 0));
for(int i=0;i<n;i++){
for(int j=0;j<=i;j++)
cin>>input[i][j];
}
cout<<maximumPathSumInTriangle(input);
}
}3 1 2 3 5 8 1
12
Java code to find Maximum path sum in a triangle
import java.util.*;
class Main{
static int maximumPathSumInTriangle(int input[][], int n)
{
// start from row above bottom row
// since the bottom row cells are the answers themselves
for(int i=n-2;i>=0;i--)
{
// start from left to right in column
for(int j=0;j<=i;j++)
{
if(input[i+1][j] > input[i+1][j+1])
input[i][j] += input[i+1][j];
else
input[i][j] += input[i+1][j+1];
}
}
return input[0][0];
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // number of rows
int input[][] = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<=i;j++)
input[i][j] = sc.nextInt();
}
int answer = maximumPathSumInTriangle(input, n);
System.out.print(answer);
}
}3 1 2 3 5 8 1
12
Complexity Analysis
Time Complexity
O(N^2), as we moved across each row and each column. In the process, we traveled to each cell. And since there were O(N^2) cells in the triangle and the transition for DP took only O(1) operation. Thus, the time complexity is also polynomial.
Space Complexity
O(N^2) since we created a 2D DP array. Thus the space complexity is also polynomial.