Table of Contents
Problem Statement
The problem “Subset with sum divisible by m” states that you are given an array of non-negative integers and an integer m. Now you need to find if there is a subset having sum divisible by m. That is the sum of the subset should give 0 as a result when we take its mode with m.
Example
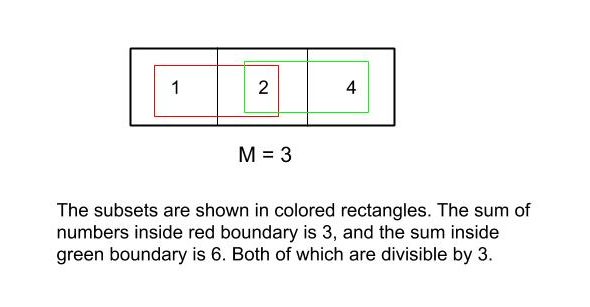
array = {1, 2, 4}
m = 3True
Explanation
Subset having values {1,2} sum to give 3 as result. {2, 4} also sum up to give 6 as a result which is also divisible by 3. Thus the answer is true.
Approach
So, we have also come across a similar problem which is to check if the sum of the subset is equal to a target Sum. But here do not check if the subset-sum is equal to a given sum but we need to check if the subset-sum is divisible by m. So we can reframe the problem as we need to find if there is a subset having sum = m, 2m, 3m, .., etc. If the subset has a sum equal to any of the given values. we return true else false.
So, instead of thinking this way. We keep on taking the mod of sum and if we somehow get a 0. We are sure that there exists a subset having sum divisible by m. But we need to care about something before that. If the number of elements n>=m(number against whose mod is to be taken). Then the answer always exists because of the Pigeonhole Principle. We only need to deal with cases having sum 0 to m-1 which is n<=m.
So, the whole idea behind this approach is that we have some subsets having sum = j, then we can create new subset having sum = (j+current_element)%m. And that’s how we are going to fill our Dynamic Programming Table.
Code
C++ code for Subset with sum divisible by m
#include<bits/stdc++.h>
using namespace std;
bool findSubsetDivisibleByM(int arr[], int n, int m)
{
// because of piegonhole principle
if (n > m)
return true;
// this will work as dp array for all elements until the last element
bool dp[m]; memset(dp, false, m);
for (int i=0; i<n; i++)
{
// this will work as our current dp array
bool tmp[m]; memset(tmp,false,m);
// we will add the current element to all possible subset sum
// until now and then take the mod of the sum and will keep
// on filling the current dp array(tmp)
for (int j=0; j<m; j++)
{
// if the dp table until the last element has subset sum = j
if (dp[j] == true)
{
if (dp[(j+arr[i]) % m] == false)
// fill the current dp table(tmp array)
tmp[(j+arr[i]) % m] = true;
}
}
// now just fill the original dp array
for (int j=0; j<m; j++)
if (tmp[j] == true)
dp[j] = true;
// fill the dp array considering you have subset made of only current element
dp[arr[i]%m] = true;
}
return dp[0];
}
int main(){
// Number of elements
int n;cin>>n;
// Number which should divide the subset
int m;cin>>m;
// array to store non-negative numbers
int a[n];
for(int i=0;i<n;i++)
cin>>a[i];
bool can = findSubsetDivisibleByM(a, n, m);
if(can == true)
cout<<"There exists a subset having sum divisible by m";
else
cout<<"There does not exist any subset having sum divisible by m";
}
3 3 1 2 4
There exists a subset having sum divisible by m
Java code for Subset with sum divisible by m
import java.util.*;
class Main{
static boolean findSubsetDivisibleByM(int arr[], int n, int m)
{
// because of piegonhole principle
if (n > m)
return true;
// this will work as dp array for all elements until the last element
boolean dp[] = new boolean [m];
for(int i=0;i<m;i++)
dp[i] = false;
for (int i=0;i<n; i++)
{
// this will work as our current dp array
boolean tmp[] = new boolean[m];
for(int j=0;j<m;j++)
tmp[j] = false;
// we will add the current element to all possible subset sum
// until now and then take the mod of the sum and will keep
// on filling the current dp array(tmp)
for (int j=0; j<m; j++)
{
// if the dp table until the last element has subset sum = j
if (dp[j] == true)
{
if (dp[(j+arr[i]) % m] == false)
// fill the current dp table(tmp array)
tmp[(j+arr[i]) % m] = true;
}
}
// now just fill the original dp array
for (int j=0; j<m; j++)
if (tmp[j] == true)
dp[j] = true;
// fill the dp array considering you have subset made of only current element
dp[arr[i]%m] = true;
}
return dp[0];
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
// Number of elements
int n = sc.nextInt();
int m = sc.nextInt();
// array to store non-negative numbers
int a[] = new int[n];
for(int i=0;i<n;i++)
a[i] = sc.nextInt();
boolean can = findSubsetDivisibleByM(a, n, m);
if(can == true)
System.out.println("There exists a subset having sum divisible by m");
else
System.out.println("There does not exist any subset having sum divisible by m");
}
}3 3 1 2 4
There exists a subset having sum divisible by m
Complexity Analysis
Time Complexity
O(M^2), because we have to solve the problem only when n<=m. Thus the upper bound for n is m. Thus the time complexity is polynomial.
Space Complexity
O(M), because the space required for the dp array is linear. Space was only required for storing the dp table and thus the space complexity is linear.