Table of Contents
Problem Statement
“Check if each internal node of a BST has exactly one child” problem states that you are given a preorder traversal of a binary search tree. And you need to find if all the non-leaf nodes contain only a single child. Here we also consider that all the nodes in the given input have distinct values.
Example
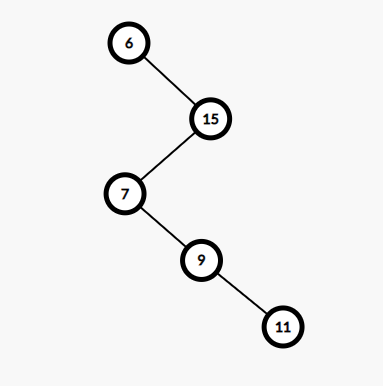
Preorder Traversal: 6 15 7 9 11
Yes
Explanation: As we can see in the image above, the tree with the given preorder traversal has a single child for each internal node. Thus the output is yes.
Approach to Check if each internal node of a BST has exactly one child
Preorder Traversal means that the root is given preference and is printed before its left and right subtree. Thus the elements after the root are either smaller or greater than the root. So, if we need to check if a given sequence is preorder of a Binary Search Tree. We can use two nested loops to check if we can create a binary search tree with the given sequence.
Naive Approach
As we already discussed, that preorder traversal contains the root at the top and after the left and right subtree are printed. Now this operation is done recursively until all the nodes in the tree are covered. So, we can check if the given sequence represents a BST, we run two nested loops where the outer loop is used to pick a root. And the nested loop checks if the elements after it can represent its left and right subtree. For that, we check if until a certain index all elements are lesser than the picked element. And elements after that are greater than the picked element. Now, we can modify this approach as per our use case.
Let’s see how can we modify the algorithm to check if each internal node of a BST has exactly one child. If the BST’s internal child has exactly one child. This means that each internal node can have either left subtree or right subtree. It won’t contain both the subtrees at the same time. Thus, to summarise our algorithm. We use two nested loops, where the outer loop picks an element. Then the nested loop is used to check if elements coming after it belongs to anyone of the subtrees. Previously, we used to have a certain index before which elements were lesser than the root, after which elements were greater than it. Now, we won’t find any such index. But this method is not efficient enough because it has a polynomial-time complexity of O(N^2).
Efficient approach
Until now, we have made one point clear that all the children of any node will be either lesser or greater than the current node as per this problem. So, to check if each internal node of a BST has exactly one child we find the next preorder successor of the current node. Then we find the last preorder successor of the current node. If both the successors are lesser than the current node or greater than the current node. Then we proceed else we know that the current node has both left and right subtree because one of the elements is smaller than the current node. And another node is larger than the current node. Thus we return false or -1 as per our requirement.
Code
C++ code to check if each internal node of a BST has exactly one child
#include<bits/stdc++.h>
using namespace std;
bool checkIfALlInternalNodesHaveSingleChild(vector<int> preorder, int i){
int n = preorder.size();
if(i==n-1)return true;
int next = preorder[i+1] - preorder[i];
int lst = preorder[n-1] - preorder[i];
int prod = next*lst;
if(prod<0)
return false;
return checkIfALlInternalNodesHaveSingleChild(preorder, i+1);
}
int main()
{
int n;cin>>n;
vector<int> preorder(n);
for(int i=0;i<n;i++)cin>>preorder[i];
cout<<(checkIfALlInternalNodesHaveSingleChild(preorder, 0) ? "Yes" : "No");
}
5 6 15 7 9 11
Yes
Java code to check if each internal node of a BST has exactly one child
import java.util.*;
import java.lang.*;
import java.io.*;
class Main
{
static boolean checkIfALlInternalNodesHaveSingleChild(int preorder[], int i){
int n = preorder.length;
if(i==n-1)return true;
int next = preorder[i+1] - preorder[i];
int lst = preorder[n-1] - preorder[i];
int prod = next*lst;
if(prod<0)
return false;
return checkIfALlInternalNodesHaveSingleChild(preorder, i+1);
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int preorder[] = new int[n];
for(int i=0;i<n;i++)preorder[i] = sc.nextInt();
boolean answer = checkIfALlInternalNodesHaveSingleChild(preorder, 0);
System.out.print(answer == true ? "Yes" : "No");
}
}5 6 15 7 9 11
Yes
Complexity Analysis
Time Complexity
O(N), since we have just traversed through the preorder array. And preorder array has N elements thus a linear time complexity.
Space Complexity
O(N), the space required for the recursive stack, and we also used an input array of size N to store the preorder sequence.