Minimum swaps to make sequences increasing

Problem Statement

“Minimum swaps to make sequences increasing” states that you are given two arrays a[ ] and b[ ] of the same size n. Swap the elements of the array a with array b to make both arrays strictly increasing. You can swap elements at the same indexes only i.e. a[i] can be swapped with b[i] only. So we need to find the minimum number of swaps that are required to make both arrays a[ ] and b[ ] strictly increasing. Print -1 if no answer exists.

Example

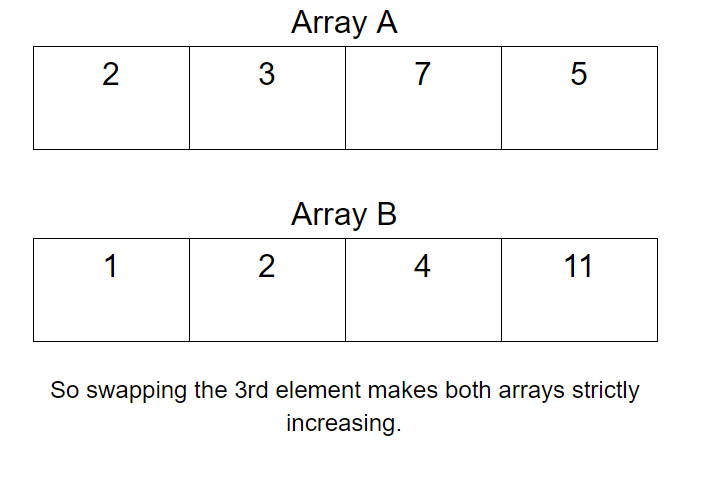
a[ ] = {2, 3, 7, 5}

b[ ] = {1, 2, 4, 11}

1

Explanation: We can swap the third element in a[] with the third element in b[], which will make both the arrays strictly increasing.

a[ ] = {1, 2, 5, 4, 9, 8}

b[ ] = {1, 2, 3, 6, 7, 11}

2

Explanation; Since we swapped the 5th element. Both the arrays are now arranged in strictly increasing order.

a[ ] = {2, 1}

b[ ] = {1, 2}

-1

Explanation: Because there is no way to swap the elements of the array a[] with b[] such that they get arranged in strictly increasing order. So, we return -1 as an answer.

Approach

Algorithm for Minimum swaps to make sequences increasing problem

1. Initialize two nonempty arrays a[ ] and b[ ] of the integer type and of the same size n.
2. Similarly, initialize an integer variable count as 0.
3. Traverse through the array elements starting from 1 till n-1.
4. Check, if the element at current index in given array a[ ] is less than or equal to the element at current index-1 in given array a[ ] or the element at current

index in given array

 b[ ] is less than or equal to the element at current index-1 in given array b[ ], swap the array element with another array element at same index and increment the count by 1.
5. After that, traverse again from 1 to n-1 and check again if the element at current index in given array a[ ] is less than or equal to the element at current index-1 in given array a[ ] or the element at current index in given array b[ ] is less than or equal to the element at current index-1 in given array b[ ], return -1.
6. Return count.

So, here we first create the arrays and initialize them. After that, we check if the current element is strictly larger than the last element in biot the arrays. If this condition is satisfied, we move ahead. But if the condition is not satisfied, we swap the elements. At this point, we increment the number of swaps. After traversing through the whole of the array, we check if both arrays are arranged in strictly increasing order? If they are then return number of swaps, else we return -1. This indicates that we were not able to rearrange the elements that make both arrays strictly increasing.

Code

C++ Program of minimum swaps to make sequences increasing

#include <bits/stdc++.h>
using namespace std;

int minSwap(int a[], int b[], int n){
    int count = 0;
    for(int i=1; i<n; i++){
        if((a[i]<=a[i-1])||(b[i]<=b[i-1])){
            swap(a[i],b[i]);
            count++;
        }
    }
    for(int i=1; i<n; i++){
        if((a[i]<=a[i-1])||(b[i]<=b[i-1])){
            return -1;
        }
    }
    return count;
}

int main() {
  int a[] = {1, 2, 5, 4, 9, 8};
  int b[] = {1, 2, 3, 6, 7, 11};
  int n = sizeof(a)/sizeof(a[0]);
  cout<<minSwap(a, b, n);
  return 0;
}

2

Java Program of minimum swaps to make sequences increasing

class Swap{
    int minSwap(int a[], int b[], int n){
        int count = 0;
        for(int i=1; i<n; i++){
            if((a[i]<=a[i-1])||(b[i]<=b[i-1])){
                a[i]=a[i]+b[i];
                b[i]=a[i]-b[i];
                a[i]=a[i]-b[i];
                count++;
            }
        }
        for(int i=1; i<n; i++){
            if((a[i]<=a[i-1])||(b[i]<=b[i-1])){
                return -1;
            }
        }
        return count;
    }
  public static void main (String[] args){
    int a[] = {1, 2, 5, 4, 9, 8};
    	int b[] = {1, 2, 3, 6, 7, 11};
    	int n = a.length;
    	Swap s = new Swap();
    	System.out.println(s.minSwap(a, b, n));
  }
}

2

Complexity Analysis

Time Complexity

O(n) where n is the number of elements in the given array a[ ].

Space Complexity

O(1) because we used the constant extra space.