Table of Contents
Problem Statement
A Newman–Shanks–Williams prime (NSW prime) is nothing but a prime number which can be represented in a specific form given the following formula:
So we need to find nth NSW prime.
Example
n = 3
7
Explanation
S0 = 1, S1 = 1, S2 = 2*S1 + S0 = 2 + 1 = 3, S3 = 2*S2 + S1 = 2*3 + 1 = 7
Approach
NSW primes were first described by Morris Newman, Daniel Shanks and Hugh C. Williams in 1981 during the study of finite simple groups with square order.
The first few NSW primes are 7, 41, 239, 9369319, 63018038201, … (sequence A088165 in the OEIS), corresponding to the indices 3, 5, 7, 19, 29, … (sequence A005850 in the OEIS). {taken from Wikipedia}
In the problem, we are given just a number n which denotes that we need to find the nth NSW prime. We can find the NSW prime using recurrence relation.
Recurrence relation
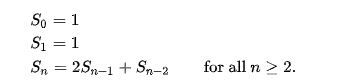
So one may use a naive approach to find the nth NSW prime. For the naive approach as we can see that each NSW prime is dependent on the last NSW prime and last to last NSW prime. So we can make use of Dynamic Programming, where we can store the last two NSW primes. Cause if we don’t save the last two NSW primes. We will be solving the problem in a recursive fashion which will result in exponential time complexity. Thus to reduce the current exponential time complexity to linear time complexity. We will memoize these values.
Code
C++ code for finding nth Newman–Shanks–Williams prime
#include <bits/stdc++.h>
using namespace std;
int main(){
// nth NSW prime which is wanted
int n;cin>>n;
if(n == 0 || n == 1)
cout<<1;
else{
int lastToLast = 1, last = 1;
int cur;
for(int i=2;i<=n;i++){
cur = 2*last + lastToLast;
lastToLast = last;
last = cur;
}
cout<<cur;
}
}4
17
Java code for finding nth Newman–Shanks–Williams prime
import java.util.*;
class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
// nth NSW prime which is wanted
int n = sc.nextInt();
if(n == 0 || n == 1)
System.out.print(1);
else{
int lastToLast = 1, last = 1;
int cur = 0;
for(int i=2;i<=n;i++){
cur = 2*last + lastToLast;
lastToLast = last;
last = cur;
}
System.out.print(cur);
}
}
}4
17
Complexity Analysis
Time Complexity
O(N), since we need to loop until we find the nth NSW prime. The time complexity is linear.
Space Complexity
O(1), because whatever the variables we have used to compute the result does not depend on the input. Thus the space complexity is constant.