Bellman Ford Algorithm is used for Finding the shortest path from the source vertex to all the vertices. Given a graph with a source vertex and weights of edges that may be negative or positive.
Now, the reader might say:
We have Dijkstra already. Why bother ourselves with another algorithm? Let me satisfy such queries with the drawbacks of Dijkstra
- It’s greedy!
- It cannot work with negative weights
- It may or may not thus give a correct answer.
Thus, In this article we aim to cover:
- How Bellman Ford algorithm works?
- The drawbacks of the Bellman Ford Algorithm.
Table of Contents
How Bellman Ford Algorithm works?
For n vertices, we relax the edges for n-1 times where n is the number of edges. Let’s now look into the relaxation equation which is the most important thing in this algorithm.
Relax(u,v):
if distance(v)>distance(u)+cost(u,v) :
distance(v)=distance(u)+cost(u,v)
Where u and v are edges.
Now that we know the relaxation equation let us go through the algorithm step by step-
- Initialize distance from the source to destination as infinity.
- Select any two edges and make the list of edges.
- Relax the edges until the shortest distance starts repeating itself or in the worst-case scenario n-1 times.
Example for Bellman Ford Algorithm
Let us understand this better by example. In the below graph, source=0, number of vertices=5
We initially assign all the distances as infinity and make a list of the edges
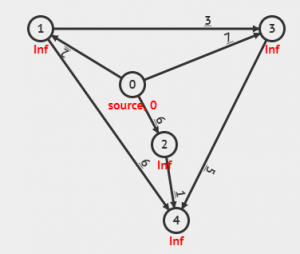
Relaxing for (0,1) we have 0+2<∞ making us update the value at 1 as 2.We similarly relax all the edges.
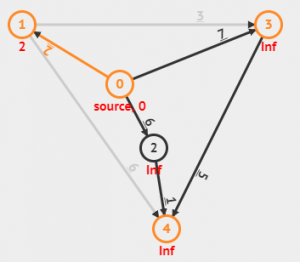
This would be the graph obtained after the first iteration
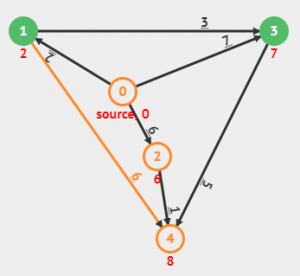
We would similarly process the graph 5 times to reach the final graph with the least distances obtained as shown in the graph below.
 Now that we have understood how the algorithm works let us implement it using code
Now that we have understood how the algorithm works let us implement it using code
Java Program for Bellman Ford Algorithm
import java.util.*;
class bellman
{
public static void bell(int graph[][],int V,int E,int src)
{
int []distance=new int[V];
//Initializing the distance to 1 for all the vertices
for(int i=1;i<V;i++)
distance[i]=Integer.MAX_VALUE;
//Relaxing all the edges V-1 times
for(int i=0;i<V;i++)
{
for(int j=0;j<E;j++)
{ //dist(v)+cost(u,v)<dist(v)
if(distance[graph[j][0]]+graph[j][2]<distance[graph[j][1]])
{
distance[graph[j][1]]=distance[graph[j][0]]+graph[j][2];
}
}
}
//Checking for negative weight cycle
for(int i=0;i<E;i++)
{
int start=graph[i][0];
int desti=graph[i][1];
int cost=graph[i][2];
if(distance[start]!=Integer.MAX_VALUE && distance[start]+cost<distance[desti])
System.out.println("Negative weight cycle detected");
}
for(int i=0;i<V;i++)
{
System.out.println("Shortest distance from 0 to:"+i+" is "+distance[i]);
}
}
public static void main(String args[])
{
int V=5;
int E=7;
int graph[][]={{0,1,2},{0,3,1},{0,2,6},
{1,3,3},{1,4,6},
{2,4,1},
{3,4,5}};
bell(graph,V,E,0);
}
}C++ Code
#include <bits/stdc++.h>
struct Edge
{
int src, dest, weight;
};
struct Graph
{
int V, E;
struct Edge* edge;
};
struct Graph* create(int V, int E)
{
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
void chkres(int dist[], int n)
{
printf("Vertex Distance from\n");
for (int i = 0; i < n; ++i)
printf("%d \t %d\n", i, dist[i]);
}
void BellmanFord(struct Graph* graph, int src)
{
int V = graph->V;
int E = graph->E;
int dist[V];
//Initalizing to infinity
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
//Relaxing all edges |V| - 1 times.
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++)
{
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
{
printf("Graph contains negative weight cycle");
return;
}
}
chkres(dist, V);
return;
}
int main()
{
int V = 4;
int E = 4;
struct Graph* graph = create(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 3;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = -2;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 1;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 0;
BellmanFord(graph, 0);
return 0;
}Vertex Distance from 0 0 1 3 2 -2 3 3
Complexity Analysis
The time complexity of this algorithm sums up to O(V*E) where V is the number of vertices and E is the number of edges in the graph.
Advantages and Real Life Applications
- Works with negative weights as well. This can work where in some cases we may get some advantage of taking a certain path. Example-While traveling to a cricket match there may be some paths where we may have to pay taxes and some paths which have the houses of our relatives who may give some money or gifts if we drop by their house.
- Works well for distributed systems
- It is a dynamic algorithm
Disadvantages of Bellman Ford Algorithm
- It can only work for directed graphs
- It only requires local information