K Empty Slots

Difficulty Level Hard
Frequently asked in Amazon Google
Array Ordered MapViews 1751

K empty slots correctly present a gardener’s dilemma, trying to pick flowers that suit our condition.

Our gardener has a field of N-slots. Mr gardener has planted a flower in each one of the slots. Each flower will bloom on a certain unique day. Also, we have planted evergreen flowers. Once they bloom, they are considered blooming forever.

The day that each of these flowers is blooming is stored in an array whose values range from 1 to N.The numbers in the array represents the day on which is going to attain the blooming status.Thus if, flower[i]=x.The xth flower will be blooming on the day i.

What is the blooming condition?

K is a number we will be taking care of. We will be finding the day on which two flowers are blooming with k non-blooming flowers between them. The mystery behind K Empty Slots is thus unlocked, or is it?

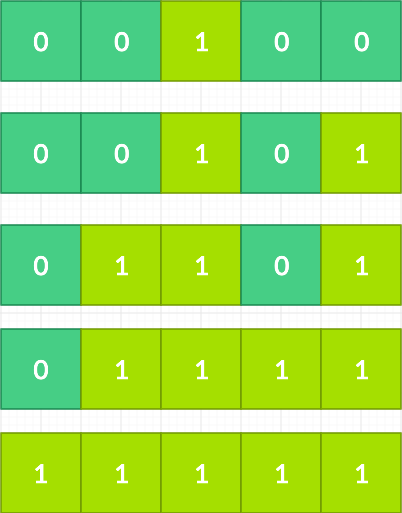
Images speak for a thousand words. So, rather than exaggerating, I will be running through a sample for an input.

Input:

Flowers:[5,3,1,4,2]

k: 1

Output:2

On the second day, the third and the fifth flower bloom leaving a flower that is still blooming.

Image illustrating the same

K Empty Slots
An illustration showing the blooming pattern

How to approach the problem?

The approach I am about to describe uses the sliding window approach. We have a wide range of problems on this topic that you can check out before we proceed on to learn further.

Without any further delay let us jump right into the solution of K Empty Slots

  • Let us create an array named days to hold the position of the flower number that is blooming on that particular day
  • Days[flower[i]-1] will hold the position i.e i+1
  • We maintain a variable min to hold the answer
  • The above two steps help us to proceed with the sliding window and hence are important for us to proceed
    • We thus start with our sliding window for K Empty Slots
    • We maintain a sliding window of size k+2
    • At any point of time if left=i then right=i+k+1
    • We check for each element if it is greater than left and right
      • As long as we are obeying this rule we continue
      • If we are not then we consider the next window
  • When we reach the end of the window we check for the maximum of left and right elements
  • The value obtained is then compared with the current value we have in the min

The process we are illustrating above is walking us through finding the perfect subarray that obeys the conditions of having late bloomers between the blooming flowers.

Java Code For K-Empty Slots

import java.util.*;
public class kslots
{
  public static int emoty(int[] blooms,int k)
  {
    int days[]=new int[blooms.length];
    for(int i=0;i<days.length;i++)
    {
      days[blooms[i]-1]=i+1;
    }
    int left  =0;
    int right =k+1;
    int min   =Integer.MAX_VALUE;
    for(int i=1;right<days.length;i++)
    {
      if(days[i]>days[left] && days[i]>days[right])
        continue;
      if(i==right)
        min=Math.min(min,Math.max(days[left],days[right]));
      left  =i;
      right =left+k+1;
    }
    if(min==Integer.MAX_VALUE)
      return -1;
    else
      return min;
  }
  public static void main(String args[])
  {
    Scanner sc=new Scanner(System.in);
    int n=sc.nextInt();
    int blooms[]=new int[n];
    for(int i=0;i<n;i++)
      blooms[i]=sc.nextInt();
    int k=sc.nextInt();
    int num=emoty(blooms,k);
    System.out.println(num);
  }
}

C++ Code for K-Empty Slots

#include<iostream>
using namespace std;
int maxs(int a,int b)
{
  if(a>b)
    return a;
  else
    return b;
}
int mins(int a,int b)
{
  if(a>b)
    return b;
  else
    return a;
}
int emoty(int blooms[],int k)
{
  unsigned int m=(sizeof(blooms)/sizeof(blooms[0]));
  int days[m];
  for(int i=0;i<m;i++)
  {
    days[blooms[i]-1]=i+1;
  }
  int left  =0;
  int right =k+1;
  int min   =9999;
  for(int i=1;right<m;i++)
  {
    if(days[i]>days[left] && days[i]>days[right])
        continue;
    if(i==right)
      min=mins(min,maxs(days[left],days[right]));
    left=i;
    right=left+k+1;
  }
  if(min=9999)
    return -1;
  else
    return min;
}
int main()
{
  int n,k;
  cin>>n;
  int blooms[n];
  for(int i=0;i<n;i++)
    cin>>blooms[i];
  cin>>k;
  int num=emoty(blooms,k);
  cout<<num;
}
[5,3,1,4,2]
1

2

Complexity Analysis

The time complexity of the algorithm=O(n)

The space complexity of the algorithm=O(n)

How is it so for K Empty Slots?

  • Iterating through the array we choose our sliding windows which is a trivial operation
  • In the worse case the sliding window may slide through each element one by one
    • This makes the run time complexity of the algorithm O(n)
    • Not just this problem but any other problem that goes by this protocol will involve O(n) time
  • The space complexity is O(n) as we create a copy of the entire array

I hope this explanation for K Empty Slots was awesome and understandable!

Keep tuning in to Tutorialcup 😀

References

Translate »