KMP(Knuth-Morris-Pratt) algorithm is used for pattern searching in a given string. We are given a string S and a pattern p, our goal is to determine whether or not the given pattern is present in the string.
Table of Contents
Example
Input:
S = “aaaab”
p = “aab”
Output:
true
Naive Approach
The naive approach for pattern searching is to match the given pattern character by character in the given string.
Example
S= “aaaab” ->Match
p= “aab”
S= “aaaab” ->Match
p= “aab”
S= “aaaab” ->Mismatch
p= “aab”
S= “aaaab” ->Match
p= “aab”
S= “aaaab” ->Match
p= “aab”
S = “aaaab” ->Mismatch
p = “aab”
S = “aaaab” ->Match
p = “aab”
S = “aaaab” ->Match
p = “aab”
S = “aaaab” ->Match
p = “aab”
Pattern p is found in S.
In the above approach we are reverting back our progress in String S on encountering a mismatch, so the time complexity of the naive pattern matching algorithm is O(length of S x length of p).
KMP Algorithm
The idea of KMP algorithm is to save the progress and eliminate the reverting back in the main String(S), it is achieved by pre-processing the given pattern(p).
The algorithm is similar to the naive approach, we start searching for pattern_p in String S, character by character, and if we encounter a mismatch, then instead of reverting back in the main string S, we revert back our position in pattern p, to a point, where the suffix is also a prefix in the matched part of the pattern.
Example
S= “abcaxabcab” ->Match
p= “abcab”
S= “abcaxabcab” ->Match
p= “abcab”
S= “abcaxabcab” ->Match
p= “abcab”
S= “abcaxabcab” ->Match
p = “abcab”
S= “abcaxabcab” ->Mismatch
p = “abcab”
At this point the matched part of pattern_p in the string s is “abca”, in this matched part “a” at index 4 is a suffix that is also a prefix(“a” at index 1), so we revert back in p to the character b(next to the prefix “a”) and continue matching.
S= “abcaxabcab” ->Mismatch
p = “abcab”
The matched part of patterns
p in string S is “a”, there is no suffix that is also a prefix, so we revert back to the first character in p and continue matching using KMP Algorithm.
S= “abcaxabcab” ->Mismatch
p = “abcab”
The mismatch occurred at index 1, so we advance in the String S.
S = “abcaxabcab” (Match)
p = “abcab”
S = “abcaxabcab” (Match)
p = “abcab”
S = “abcaxabcab” (Match)
p = “abcab”
S = “abcaxabcab” (Match)
p = “abcab”
S = “abcaxabcab” (Match)
p = “abcab”
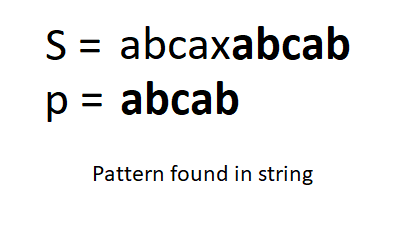
We have found p in S.
Algorithm
- Create an array named table, of size equals to the length of pattern_p, table[i] stores the length of the longest suffix that is also a prefix from index 1 to i.
- Initialize table[0] = 0, because for index 0, there is no suffix which is also a prefix
- Initialize i = 0 and j = 1, run a loop while j < n(length of pattern_p), repeat steps 4 and 5
- If p[i] and p[j] matches, table[j] = i + 1, increment i and j
- If p[i] and p[j] mismatches, and i is not equals to 0, i = table[i – 1], and if i = 0, then table[j] = 0 and increment j
Pseudo Code for KMP Algorithm
table[0] = 0
i = 0, j = 1
while (j < n) { // n is the length of pattern p
if (p[i] == p[j]) {
table[j] = i + 1;
i++;
j++;
} else {
if (i != 0) {
i = table[i - 1];
// Do not increment j here
} else {
table[j] = 0;
j++;
}
}
}Examples
pattern : “aaab”
table[] = {0, 1, 2, 0}
pattern : ” dsgwadsgz”
table = {0, 0, 0, 0, 0, 1, 2, 3, 0}
Algorithm
- Pre-process the pattern to create the prefix-suffix table array as mentioned above.
- We start matching the given string and pattern starting from the first character and keep incrementing in both the strings till we are matching the characters if we matched all the characters, the pattern is found and we stop.
- As we see a mismatch, let mismatch occurs at index i in the pattern, we revert back to table[i – 1] index in the pattern or at index 0 if the mismatch occurs at index 0.
- Repeat steps 2 and 3, till we traverse the whole string or we found the pattern.
JAVA Code for KMP Algorithm
public class KMPAlgorithm {
// Function to pre-process the pattern and to create the suffix-prefix table
private static void preProcess(char[] p, int[] table, int n) {
// Initialize table[0] as 0
table[0] = 0;
// Initialise i = 0 and j = 1
int i = 0, j = 1;
// Run a loop till length of pattern, if p[i] and p[j] matches table[j] = i + 1 else table[j] = 0
while (j < n) {
if (p[j] == p[i]) {
// Match found set table[i] = i + 1, and advance i and j
table[j] = i + 1;
i++; j++;
} else {
if (i != 0) {
i = table[i - 1];
// We do not increment j here
} else {
table[j] = 0;
j++;
}
}
}
}
public static void main(String[] args) {
char S[] = "abcaabcab".toCharArray();
char p[] = "abcab".toCharArray();
// Pre-process the pattern
int table[] = new int[p.length];
preProcess(p, table, p.length);
// Searching the pattern in the given string
int i = 0; // index for string
int j = 0; // index for pattern
boolean found = false; // Boolean variable to indicate that the pattern is found or not
while (i < S.length) {
if (S[i] == p[j]) {
// Advance forward the characters are same
i++;
j++;
} else {
// Characters are not same, revert back the progress in the pattern
if (j !=0) // Reset the position of j in the pattern, do no advance in string
j = table[j - 1];
else // first character is mis-matched, advance in the string
i++;
}
if (j == p.length) {
// The pattern is found in the string
found = true;
break;
}
}
if (found)
System.out.println("true");
else
System.out.println("false");
}
}true
C++ Code for KMP Algorithm
#include <bits/stdc++.h>
using namespace std;
void preProcess(char *p, int *table, int n) {
// Initialize table[0] as 0
table[0] = 0;
// Initialise i = 0 and j = 1
int i = 0, j = 1;
// Run a loop till length of pattern, if p[i] and p[j] matches table[j] = i + 1 else table[j] = 0
while (j < n) {
if (p[i] == p[j]) {
// Match found set table[i] = i + 1, and advance i and j
table[j] = i + 1;
i++;
j++;
} else {
if (i != 0) {
i = table[i - 1];
// We do not increment j here
} else {
table[j] = 0;
j++;
}
}
}
}
int main() {
char s[] = "abcaabcab";
char p[] = "abcab";
int n = strlen(s);
int m = strlen(p);
// Pre-process the pattern
int table[m];
preProcess(p, table, m);
// Searching the pattern in the given string
int i = 0; // index for string
int j = 0; // index for pattern
bool found = false; // Boolean variable to indicate that the pattern is found or not
while (i < n) {
if (s[i] == p[j]) {
// Advance forward the characters are same
i++;
j++;
} else {
// Characters are not same, revert back the progress in the pattern
if (j != 0) {
// Reset the position of j in the pattern, do no advance in string
j = table[j - 1];
} else {
// first character is mis-matched, advance in the string
i++;
}
}
if (j == m) {
// The pattern is found in the string
found = true;
break;
}
}
if (found)
cout<<"true"<<endl;
else
cout<<"false"<<endl;
return 0;
}true
Complexity Analysis for KMP Algorithm
In KMP algorithm there is no reverting back in the String S, so the time complexity is of the order of length of S and it is also proportional to the length of pattern_p, for preprocessing, therefore,
Time Complexity = O(length of String S + length of Pattern p)