Prim's Algorithm - Prim’s Minimum Spanning Tree Prim's Algorithm

Prim’s algorithm is used to find the Minimum Spanning Tree(MST) of a connected or undirected graph. Spanning Tree of a graph is a subgraph that is also a tree and includes all the vertices. Minimum Spanning Tree is the spanning tree with a minimum edge weight sum.

Table of Contents

Example

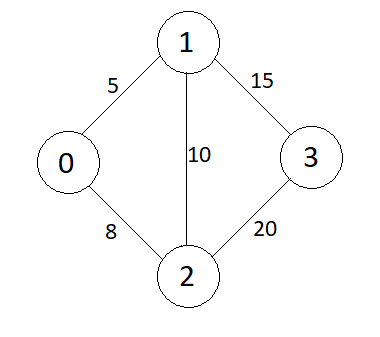
Graph

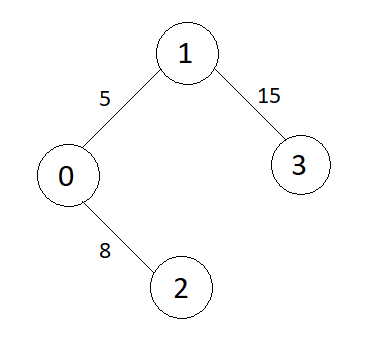
Prim's Algorithm

Minimum Spanning Tree(MST)

Prim's Algorithm

Algorithm for Prim’s Algorithm

Prim’s algorithm is a greedy algorithm that maintains two sets, one represents the vertices included( in MST ), and the other represents the vertices not included ( in MST ).
At every step, it finds the minimum weight edge that connects vertices of set 1 to vertices of set 2 and includes the vertex on other side of edge to set 1(or MST).
The group of edges that connects a set of vertices to another set of vertices is known as cut in graph theory, so Prim’s algorithm finds the minimum weight edge in the cut and include the vertex on this edge in MST and repeats this process till all the vertices are included in the MST.

Create an array includedMST, that represents whether or not the current vertex is included ( in MST ).
Create another array minEdgeCut, that represents the minimum weight edge in the cut from the current vertex.
Initialize minEdgeCut as INFINITE for all the vertices and 0 for the first vertex.
Pick a vertex(say u) with minEdgeCut value, that is not included ( in MST ) and include it in MST.
Update the values of minEdgeCut for all the adjacent vertices that are not included( in MST ) for the picked vertex.
To update values, for every adjacent vertex v, if the weight of edge u-v is less than the current minEdgeCut value of v, update the minEdgeCut value as the weight of the u-v.
Repeat steps 4, 5, and 6 till all the vertices are not included.

Explanation for Prim’s Algorithm

Consider the graph shown in the image below, let’s apply the above algorithm to find the MST.

Prim's Algorithm

Initially, there is no vertex in MST so
includedMST[] = { false, false, false, false }
minEdgeCut[] = {0, INFINITE, INFINITE, INFINITE }

The vertex with minEdgeCut value, which is not included in MST is picked, that is, vertex 0, include it in MST and update the minEdgeCut value of its adjacent. So,
includedMST[] = { true, false, false, false }
minEdgeCut[] = { 0, 5, 8, INFINITE}

Vertex 1 is picked this time as it is not included in MST and has the minimum minEdgeCut value, include it in MST and update the adjacent of it. So,
includedMST[] = { true, true, false, false }
minEdgeCut[] = { 0, 5, 8, 15}

Vertex 2 is picked. Include it in MST and update the adjacent. So,
includedMST[] = { true, true, true, false }
minEdgeCut[] = { 0, 5, 8, 15}

Vertex 3 is picked. Include it in MST and update the adjacent. So,
includedMST[] = { true, true, true, true }
minEdgeCut[] = {0, 5, 8, 15 }

Prim's Algorithm

All the vertices are included in MST, so we stop.

JAVA Code for Prim’s Algorithm

import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;

public class PrimsAlgorithm {
    private static void findPrintMST(ArrayList<Edge> graph[]) {
        int n = graph.length;
        // parent array stores the parent vertex of the current vertex in MST
        int parent[] = new int[n];
        int minEdgeCut[] = new int[n];
        boolean includedMST[] = new boolean[n];

        // Initialise all minEdgeCut values as INFINITE and all vertices as not included in MST
        for (int i = 0; i < n; i++) {
            minEdgeCut[i] = Integer.MAX_VALUE;
            includedMST[i] = false;
        }

        // Initialise minEdgeCut value of first vertex as 0
        minEdgeCut[0] = 0;
        parent[0] = -1;

        // Create a min heap to pick the smallest minEdgeCut value at every step
        // Min heap of vertex and corresponding minEdgeCut value
        PriorityQueue<Element> minHeap = new PriorityQueue<>(new Comparator<Element>() {
            @Override
            public int compare(Element o1, Element o2) {
                return Integer.compare(o1.minEdgeCutValue, o2.minEdgeCutValue);
            }
        });
        for (int i = 0; i < n; i++)
            minHeap.add(new Element(i, minEdgeCut[i]));

        // While all vertices are not included in MST
        while(!minHeap.isEmpty()) {
            // Select the vertex with minimum minEdgeCut value
            int u = minHeap.poll().vertex;

            // Update minEdgeCut value for all adjacent vertices
            for (int j = 0; j < graph[u].size(); j++) {
                Edge curr = graph[u].get(j);
                // If weight of edge u-v is less than the current minEdgeCut value of v
                // update the minEdgeCut value as weight of u-v
                if (minEdgeCut[curr.to] > curr.weight && !includedMST[curr.to]) {
                    minEdgeCut[curr.to] = curr.weight;
                    parent[curr.to] = u;
                }
            }
        }

        // Print MST
        for (int i = 1; i < n; i++) {
            System.out.println("Edge from " + parent[i] + " to " + i + " weight " + minEdgeCut[i]);
        }
    }

    public static void main(String[] args) {
        // Graph
        ArrayList<Edge> graph[] = new ArrayList[4];
        for (int i = 0; i < 4; i++)
            graph[i] = new ArrayList<>();

        // Make the graph in given example
        graph[0].add(new Edge(1, 5));
        graph[0].add(new Edge(2, 8));
        graph[1].add(new Edge(0, 5));
        graph[1].add(new Edge(2, 10));
        graph[1].add(new Edge(3, 15));
        graph[2].add(new Edge(0, 8));
        graph[2].add(new Edge(1, 10));
        graph[2].add(new Edge(3, 20));
        graph[3].add(new Edge(1, 15));
        graph[3].add(new Edge(2, 20));

        // Find MST using Prim's Algorithm and print it
        findPrintMST(graph);
    }

    // Class representing an edge in the graph
    static class Edge {
        int to;
        int weight;

        public Edge(int to, int weight) {
            this.to = to;
            this.weight = weight;
        }
    }

    // Class representing pair of vertex and its minEdgeCut value
    // Used in minHeap in Prim's Algorithm for MST
    static class Element {
        int vertex;
        int minEdgeCutValue;

        public Element(int vertex, int minEdgeCutValue) {
            this.vertex = vertex;
            this.minEdgeCutValue = minEdgeCutValue;
        }
    }
}

C++ Code for Prim’s Algorithm

#include <bits/stdc++.h>
using namespace std;

// Class representing pair of vertex and its minEdgeCut value
// Used in minHeap in Prim's Algorithm for MST
class Element {
    public:
    int vertex;
    int minEdgeCutValue;
    Element(int v, int value) {
        vertex = v;
        minEdgeCutValue = value;
    }
};

// Class representing an edge in the graph
class Edge {
    public:
    int to;
    int weight;
    Edge(int t, int w) {
        to = t;
        weight = w;
    }
};

// Comparator to sort Element according to minEdgeCutValue
struct ElementComp {
    bool operator ()(const Element& e1, const Element& e2) {
        return (e2.minEdgeCutValue < e1.minEdgeCutValue);
    }
};

void findPrintMST(vector<Edge> graph[], int n) {
    // parent array stores the parent vertex of the current vertex in MST
    int parent[n];
    int minEdgeCut[n];
    bool includedMST[n];
    
    // Initialise all minEdgeCut values as INFINITE and all vertices as not included in MST
    for (int i = 0; i < n; i++) {
        minEdgeCut[i] = INT_MAX;
        includedMST[i] = false;
    }
    
    // Initialise minEdgeCut value of first vertex as 0
    minEdgeCut[0] = 0;
    parent[0] = -1;
    
    // Create a min heap to pick the smallest minEdgeCut value at every step
    // Min heap of vertex and corresponding minEdgeCut value
    priority_queue<Element, vector<Element>, ElementComp> minHeap;
    for (int i = 0; i < n; i++) {
        Element ele(i, minEdgeCut[i]);
        minHeap.push(ele);
    }
    
    // While all vertices are not included in MST
    while (minHeap.size() != 0) {
        // Select the vertex with minimum minEdgeCut value
        int u = minHeap.top().vertex;
        minHeap.pop();
        
        // Update minEdgeCut value for all adjacent vertices
        for (int j = 0; j < graph[u].size(); j++) {
            Edge curr = graph[u][j];
            // If weight of edge u-v is less than the current minEdgeCut value of v
            // update the minEdgeCut value as weight of u-v
            if (minEdgeCut[curr.to] > curr.weight && includedMST[curr.to] == false) {
                minEdgeCut[curr.to] = curr.weight;
                parent[curr.to] = u;
            }
        }
    }
    
    // Print MST
    for (int i = 1; i < n; i++) {
        cout<<"Edge from "<<parent[i]<<" to "<<i<<" weight "<<minEdgeCut[i]<<endl;
    }
}

int main() {
    vector<Edge> graph[4];
    
    // Make the graph in given example
    Edge e1(1, 5);
    Edge e2(2, 8);
    Edge e3(0, 5);
    Edge e4(2, 10);
    Edge e5(3, 15);
    Edge e6(0, 8);
    Edge e7(1, 10);
    Edge e8(3, 20);
    Edge e9(1, 15);
    Edge e10(2, 20);
    
    graph[0].push_back(e1);
    graph[0].push_back(e2);
    graph[1].push_back(e3);
    graph[1].push_back(e4);
    graph[1].push_back(e5);
    graph[2].push_back(e6);
    graph[2].push_back(e7);
    graph[2].push_back(e8);
    graph[3].push_back(e9);
    graph[3].push_back(e10);
    
    // Find MST using Prim's Algorithm and print it
    findPrintMST(graph, 4);
    
    return 0;
}

Edge from 0 to 1 weight 5
Edge from 0 to 2 weight 8
Edge from 1 to 3 weight 15

Complexity Analysis

Time Complexity = O(E log(V)), where E –> Number of edges and V –> Number of vertices.

Space Complexity = O(E + V) because we create an adjacency list that has E edges and V vertices.

References