Shuffle an Array

Given an array or set which contains n elements. Here the elements are unique or there is no repetition. Shuffle an array(or a set) of numbers without duplicates.

Example

// Init an array with set 2, 4, 3 and 1.

int[] nums = {2, 4, 3, 1};

Shuffle object = new Shuffle(nums);

// Shuffle the array [2, 4, 3, 1] and return its result. Any permutation of [2, 4, 3, 1] must equally likely to be returned, for example [4, 2, 1, 3] object.shuffle();

// Resets the array back to its original configuration of array i.e., [2, 4, 3, 1].

solution.reset();

We can do this using in O(n) time complexity by using two hashmaps.

Data Structures Used for Shuffle an Array

Map M( to store value, index pair)

Map K(to store value, changed index)

Vector arr to store current elements present in the array.

For example:

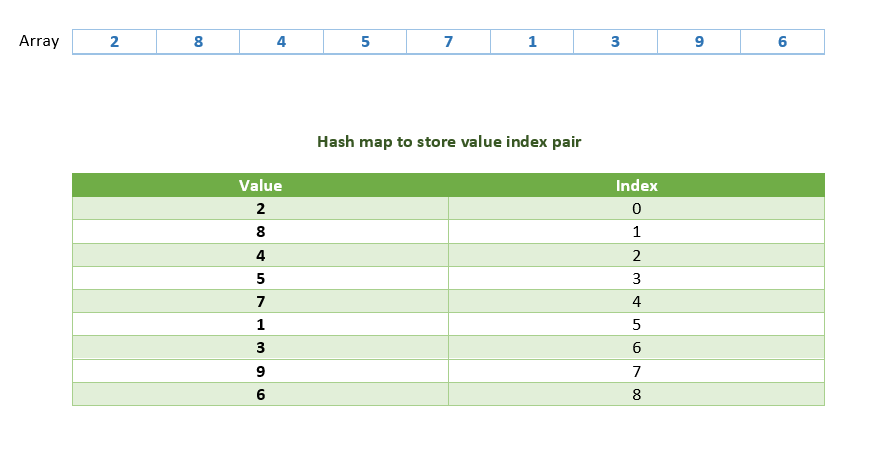
Algorithm for Constructor Function

1. For every element present in the given array nums:
   1. arr[i] = nums[i]
   2. insert the key value pair (nums[i], i) in K.
   3. insert the key value pair(nums[i], i) in M.

Algorithm for reset()

1. For every entry present in map M( iterator it ):
   1. arr[it.second] = arr[it.first], update the vector with original values.
2. Return arr.

Algorithm for shuffle()

1. Run a loop from n to 0:
   1. Select a random index (index) in range(0, n).
   2. Take the element present at index and swap it with the last element present in the array.
   3. Update the hash values for the index element and last element in map K.
2. Return arr.

Implementation

C++ program for Shuffle an Array

#include<bits/stdc++.h>
using namespace std;
class Shuffle {
public:
    vector<int> arr;
    unordered_map<int,int> m;
    unordered_map<int,int> k;
    Shuffle(vector<int>& nums) {
        for(int i=0;i<nums.size();i++){
            arr.push_back(nums[i]);
            m.insert({nums[i],i});
            k.insert({nums[i],i});
        }
    }
    /** Resets the array to its original configuration and return it. */
    vector<int> reset() {
        for(auto it:m){
            arr[it.second]=it.first;
        }
        return arr;
    }
    
    /** Returns a random shuffling of the array. */
    vector<int> shuffle() {
        int n=arr.size();
        while(n){
            int in=rand()%n;
            int index= k[arr[n-1]];
            k[arr[n-1]]=k[arr[in]];
            k[arr[in]]=index;
            swap(arr[in],arr[n-1]);
            n--;
        }
        return arr;
    }
};

int main()
{
    vector<int> nums = {2,3,4,1,5,6};
    Shuffle* obj = new Shuffle(nums);
    cout<<"Original array:\n";
    for(int i=0;i<nums.size();i++){
        cout<<nums[i]<<" ";
    }
    vector<int> _shuffle = obj->shuffle();
    cout<<"\nArray after shuffle:\n";
    for(int i=0;i<_shuffle.size();i++){
        cout<<_shuffle[i]<<" ";
    }
    vector<int> _reset = obj->reset();
    cout<<"\nArray after reset:\n";
    for(int i=0;i<_reset.size();i++){
        cout<<_reset[i]<<" ";
    }
    return 0;
}

Original array:
2 3 4 1 5 6 
Array after shuffle:
2 4 1 5 6 3 
Array after reset:
2 3 4 1 5 6 

JAVA program for Shuffle an Array

import java.util.*;
class Shuffle {
    HashMap<Integer, Integer> m,k;
    int[] arr;

    public Shuffle(int[] nums) {
        m = new HashMap<>();
        k = new HashMap<>();
        int n=nums.length;
        arr = new int[n];
        for(int i=0;i<n;i++){
            arr[i]=nums[i];
            m.put(nums[i],i);
            k.put(nums[i],i);
        }
    }
    
    /** Resets the array to its original configuration and return it. */
    public int[] reset() {
        for(Map.Entry<Integer, Integer> it : m.entrySet()){
            arr[it.getValue()]=it.getKey();
        }
        return arr;
    }
    
    /** Returns a random shuffling of the array. */
    public int[] shuffle() {
        int n=arr.length;
        Random rand = new Random(); 
        while(n>0){
            int in=rand.nextInt(n);
            int index = k.get(arr[n-1]);
            k.put(arr[n-1],k.get(arr[in]));
            k.put(arr[in],index);
            int temp = arr[in];
            arr[in] = arr[n-1];
            arr[n-1] = temp;
            n--;
        }
        return arr;
    }
}
public class Main
{
  public static void main(String[] args) {
      int[] nums = {2,3,4,6};
        Shuffle obj = new Shuffle(nums);
        System.out.print("Original array:\n");
        for(int i=0;i<nums.length;i++){
            System.out.print(nums[i]+" ");
        }
        int[] _shuffle = obj.shuffle();
        System.out.print("\nArray after shuffle:\n");
        for(int i=0;i<_shuffle.length;i++){
            System.out.print(_shuffle[i]+" ");
        }
        int[] _reset = obj.reset();
        System.out.print("\nArray after reset:\n");
        for(int i=0;i<_reset.length;i++){
            System.out.print(_reset[i]+" ");
        }
  }
}

Original array:
2 3 4 6 1 0 1 0 
Array after shuffle:
4 6 2 3 
Array after reset:
2 3 4 6 

Complexity Analysis for Shuffle an Array

Time complexity

O(n) all function i.e., Constructor function, shuffle(), reset() as all function need traversal of array only once. That’s why it leads us to linear time complexity.

Space complexity

O(n), we need 2 auxiliary hashmaps of size n to store value index pair.

References