Count pairs from two sorted arrays whose sum is equal to a given value x

Problem Statement

“Count pairs from two sorted arrays whose sum is equal to a given value x” problem states that you are given two sorted arrays of integers and an integer value called sum. The problem statement asks to find out the total number of pair which sums up to a given value.

Example

arr1[] = {1, 6, 8, 11}

arr2[] = {1, 3, 5, 9}

sum = 9

2

Explanation: Because there are a total of 2 pairs in a given array that is (6, 3) and (8, 1). Because other pairs have sum either greater or less than the required sum.

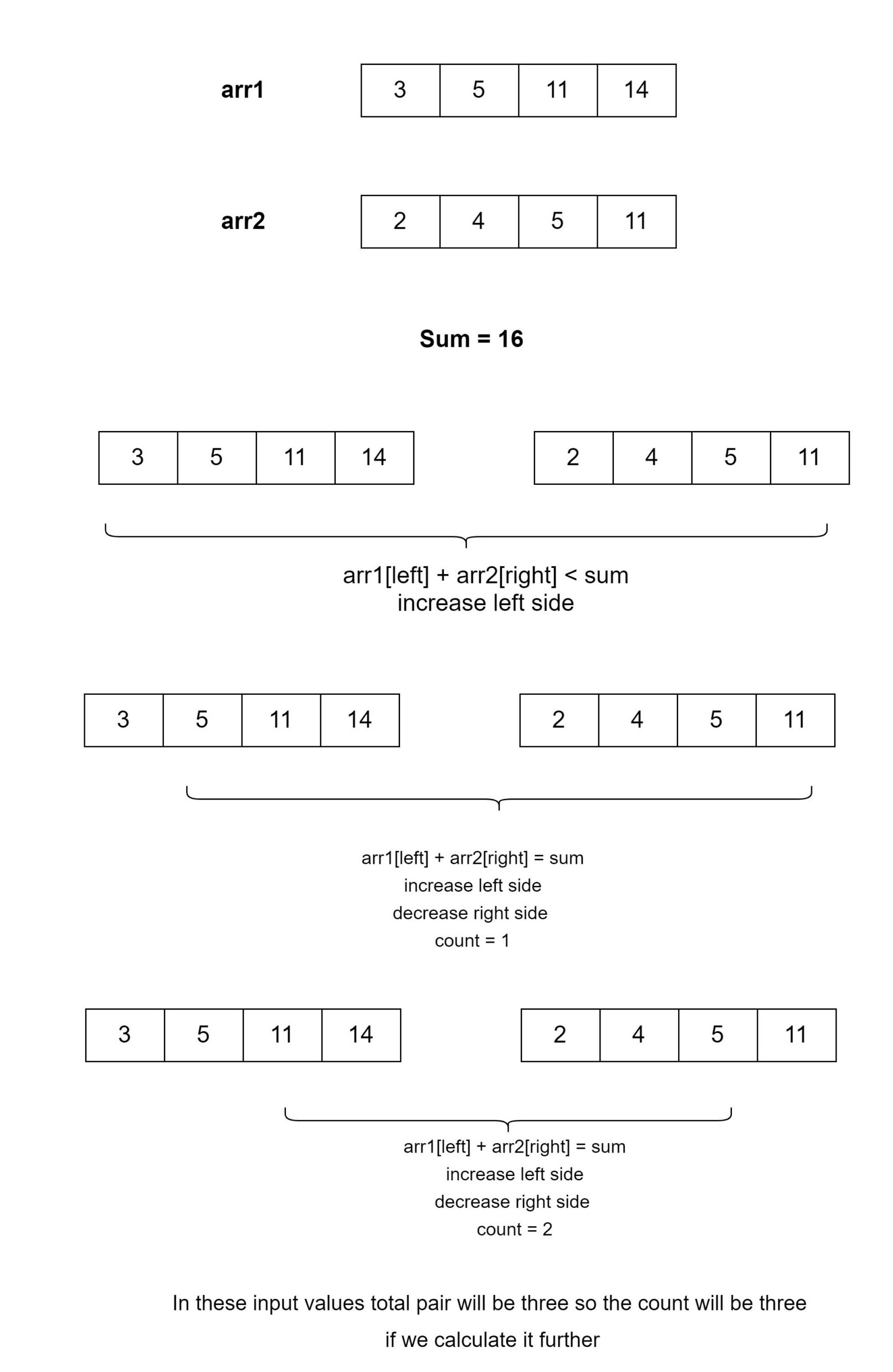
arr1[] = {3, 5, 11, 14};

arr2[] = {2, 4, 5, 11}

sum = 16

3

Explanation: Because there are a total of 3 pairs in the given array that is (5, 11), (11, 5), and (14, 2).

Algorithm to count pairs from two sorted arrays whose sum is equal to a given value x

1. Set count and left to 0, and right to n-1 where n is the length of the array.
2. While left is less than m and right is greater than equal to 0, repeat the following the steps-
    1. If the sum of arr[left] and arr[right] is equal to the given value, then increase the value of count and left by 1 and decrease the value of right by 1.
    2. Else check if the addition of arr[left] and arr[right] is less than the given value sum, then increase the value of left by 1.
    3. Decrease the value of right by 1 if the addition is greater than the sum.
3. Return the count value after traversing the arrays.

Explanation

You are given two sorted integer arrays and an integer value called sum. And we are asked to find out how many possible pairs can be formed which sums up to a given value. So, we are going to use a similar technique as a binary search method. This is also the reason why we are taking input values in increasing order. In this way, we will be able to apply that technique in solving this question. Else we would’ve sorted the array.

We are going to set the value of count to 0. Because we will be increasing that value of count by 1 if we find the required pair. A pair will be consisting of two values. Of course, we are going to check if the addition of that value in a pair is equal to the given value sum. If it is true we will increase the value of count by 1. We will run a while loop in this manner. Then it will go until the values of m (m is the length of one of the array) and r (where r is one less than the length of an array) is greater than equal to 0.

In a loop, we will check for if the value of the pair adds up to the given value. Then, we have found one pair whenever this condition becomes true. We will continue the loop if the sum is less than the given value. Then we will increase the value of l by 1 else we just decrease the value of r by 1. In the end, we will return the value of count.

Code

C++ code to count pairs whose sum is x from two sorted arrays

#include<iostream>

using namespace std;

int getPairofsum(int arr1[], int arr2[], int m, int n, int sum)
{
    int count = 0;
    int left = 0, right = n - 1;

    while (left < m && right >= 0)
    {
        if ((arr1[left] + arr2[right]) == sum)
        {
            left++;
            right--;
            count++;
        }
        else if ((arr1[left] + arr2[right]) < sum)
            left++;
        else
            right--;
    }
    return count;
}
int main()
{
    int arr1[] = {1, 6, 8, 11};
    int arr2[] = {1, 3, 5, 9};
    int m = sizeof(arr1) / sizeof(arr1[0]);
    int n = sizeof(arr2) / sizeof(arr2[0]);
    int sum = 9;
    cout << "Count = "<< getPairofsum(arr1, arr2, m, n, sum);
    return 0;
}

Count = 2

Java code to count pairs whose sum is x from two sorted arrays

class PairofSum
{
    public static int getPairofsum(int arr1[],int arr2[], int m, int n, int sum)
    {
        int count = 0;
        int left = 0, right = n - 1;

        while (left < m && right >= 0)
        {
            if ((arr1[left] + arr2[right]) == sum)
            {
                left++;
                right--;
                count++;
            }
            else if ((arr1[left] + arr2[right]) < sum)
                left++;
            else
                right--;
        }
        return count;
    }
    public static void main (String[] args)
    {
        int arr1[] = {1, 6, 8, 11};
        int arr2[] = {1, 3, 5, 9};
        int m = arr1.length;
        int n = arr2.length;
        int sum = 9;
        System.out.println( "Count = "+ getPairofsum(arr1, arr2, m, n, sum));
    }
}

Count = 2

Complexity Analysis

Time Complexity

O(m + n) where “m” and “n” is the number of elements in the arr1 and arr2. Because the max we can travel is m+n.

Space Complexity

O(1) as no extra space is required. Thus a constant space complexity is achieved.