Delete And Earn

In delete and earn problem we have given an array nums, you may perform the following operation on the array elements. In one operation you can choose any array element(say nums[i]) and get points equal to that element and delete all the occurrences of (nums[i] – 1) and (nums[i] + 1). What are the maximum points you can earn by applying these operations? Given that the maximum value in the nums array is less than or equals to 10000.

Examples

Input
nums[] = {3, 4, 2}
Output
6
Explanation
Choose 4 and delete 3, then choose 2, total points = 4 + 2 = 6

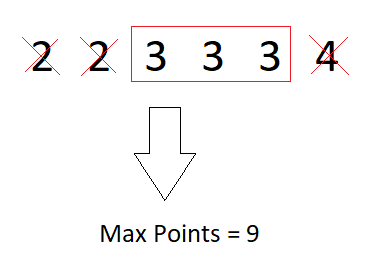
Input
nums[] = {2, 2, 3, 3, 3, 4}
Output
9
Explanation
Choose 3 and delete all 2 and 4, again choose the remaining 3, total = 3 + 3 + 3 = 9

Algorithm for Delete And Earn

Here we using the dynamic programming approach to solve delete and earn problems in the smartest way. While choosing an element it is always optimal to choose all the occurrences of that element, that is, if there are 3 elements equals to 5 in nums array, it is always optimal to choose all the three 5.

Create an array freq of size 10001(maximum value in nums array), where freq[i] stores the frequency of element i in the nums array.
Create an array dp of size 10001, where dp[i] represents the maximum points earned if nums array had only elements from i to 10000.
If an element i is chosen, then the points earned are (freq[i] * i + dp[i + 2]) and if the element is discarded the points earned are dp[i + 1], the value of dp[i] is maximum of these two, that is,
dp[i] = max((freq[i] * i + dp[i + 2]), dp[i + 1])

1. Create a freq array of size 10001, where freq[i] denotes the frequency of element ‘i’ in nums array.
2. Create an array dp of size 10001, where dp[i] denotes the maximum points earned if nums array had only elements from i to 10000.
3. The value of dp[10000] equals to freq[10000].
4. To fill the remaining elements of dp array, traverse from 9999 to 1, and at every step the value of dp[i] = max(freq[i] * i + dp[i + 2], dp[i + 1]).
5. The maximum value in the dp array is the required answer.

Implementation

JAVA code for delete and earn

public class DeleteAndEarn {
    private static int deleteAndEarn(int[] nums) {
        int n = nums.length;

        // Count the freq
        int freq[] = new int[10001];
        for (int i = 0; i < n; i++) {
            freq[nums[i]]++;
        }

        int dp[] = new int[10001];
        // Value of dp[10000] = freq[10000]
        dp[10000] = freq[10000];
        // max stores the maximum value of points earned
        int max = dp[10000];
        
        // Traverse from 9999 to 1 and find the value of dp[i]
        for (int i = 9999; i >= 0; i--) {
            // Take this
            int taking;
            if (i + 2 <= 10000) {
                taking = (freq[i] * i) + dp[i + 2];
            } else {
                taking = (freq[i] * i);
            }

            // Do not take this
            int notTaking = dp[i + 1];

            // Assign the max value
            dp[i] = Math.max(taking, notTaking);
            // Update the max value
            max = Math.max(max, dp[i]);
        }
        
        // return the max earn
        return max;
    }

    public static void main(String[] args) {
        // Example 1
        int nums1[] = new int[] {3, 4, 2};
        System.out.println(deleteAndEarn(nums1));
        
        // Example 2
        int nums2[] = new int[] {2, 2, 3, 3, 3, 4};
        System.out.println(deleteAndEarn(nums2));
    }
}

6
9

C++ code for delete and earn

#include<bits/stdc++.h> 
using namespace std;

int deleteAndEarn(int *nums, int n) {
    // Count the freq
    int freq[10001];
    for (int i = 0; i < 10001; i++)
        freq[i] = 0;
    for (int i = 0; i < n; i++) {
        freq[nums[i]]++;
    }
    
    int dp[10001];
    
    // Value of dp[10000] = freq[10000]
    dp[10000] = freq[10000];
    // max stores the maximum value of points earned
    int max = dp[10000];
    // Traverse from 9999 to 1 and find the value of dp[i]
    for (int i = 9999; i >= 0; i--) {
        // Take this
        int taking;
        if (i + 2 <= 10000) {
            taking = (freq[i] * i) + dp[i + 2];
        } else {
            taking = (freq[i] * i);
        }
        
        // Do not take this
        int notTaking = dp[i + 1];
        
        // Assign the max value
        dp[i] = std::max(taking, notTaking);
        // Update the max value
        max = std::max(max, dp[i]);
    }

    // return the max earn    
    return max;
}

int main() {
    // Example 1
    int nums1[] = {3, 4, 2};
    cout<<deleteAndEarn(nums1, sizeof(nums1) / sizeof(nums1[0]))<<endl;

    // Example 2
    int nums2[] = {2, 2, 3, 3, 3, 4};
    cout<<deleteAndEarn(nums2, sizeof(nums2) / sizeof(nums2[0]))<<endl;
    return 0;
}

6
9

Complexity analysis for delete and earn

Time Complexity = O(m + n)
Space Complexity = O(m)
where m is the maximum element in nums array and n is the length of nums array given in the delete and earn problem.

References