Distinct adjacent elements in an array

Difficulty Level Easy
Frequently asked in Coursera DE Shaw Hike IBM Kuliza Nagarro Opera OYO Rooms Zoho
ArrayViews 3394

Problem Statement

Suppose we have an integer array. The problem “Distinct adjacent elements in an array” asks to determine if it is possible to get the array in which all the adjacent numbers are distinct or not by swapping up two adjacent or neighbour elements in an array if it is possible then print “YES” else print “NO”.

Example

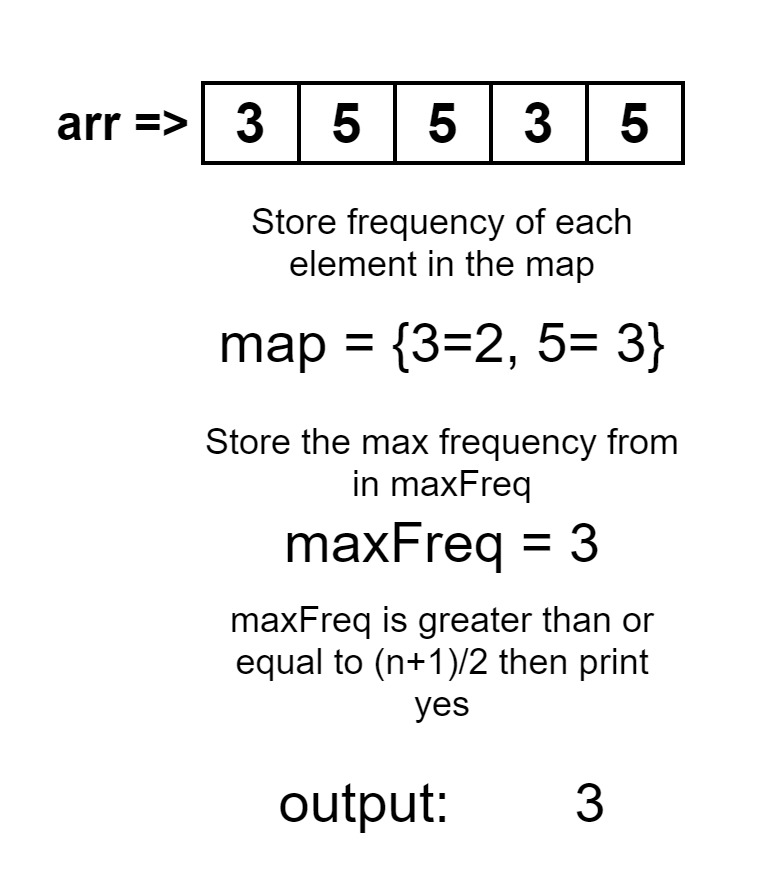
arr[] = { 3,5,5,3,5}
YES

In this example, we can get the array of distinct adjacent numbers by swapping up the arr[2] and arr[3] as 5 and 2 respectively.

Distinct adjacent elements in an array

arr[] = {3 , 5,  3, 3 }
NO

Explanation

We cannot get the desired array even after swapping up the values.

Algorithm for Distinct adjacent elements in an array

1. Declare a map.
2. Count and store the frequencies of each element of the array.
3. Set maxFreq to 0.
4. Get the maximum frequency of a number from the map.
5. Check if maxFreq is greater than the half-length of the array, means maxFreq >(n+1) / 2.
    1. If true, then print NO.
    2. Else print YES.

Explanation

We are given an integer array. We have been asked to determine if we get the array in which the distinct adjacent elements are possible. It means that if such an array is not possible then print the NO else print YES. Now, we need to check how many numbers are to be swapped to get the desired array. We need to check the occurrence of each element and also that the maximum occurrence should not be greater than half of the length of the array. If the length of an array will be given as 5. If an element has 3 occurrences in an array. Then it will be possible to rearrange the array at the first, third, and fifth position. So it would be possible to get distinct adjacent elements in an array.

We are going to do is to declare a map. We will then traverse the array and count the frequency of each element. Simultaneously store all the frequencies of each element in a map. Suppose we have an array of 5 numbers, in which two of them occurred two times in an array and another number occurred one time. So we will be storing the frequency of each element of the array. After storing all the frequencies of the element. We will set the maxFreq variable to 0. In which we are going to store the maximum frequency number of an element, after finding out the maximum frequency.

For that, we will be traversing the map, and check for each element, if we have a frequency greater than the previously stored frequency. With this, we will have the maximum number as a frequency, and check if that frequency is greater than the half of the length of the array. If true, then print NO, else print YES.

Code

C++ code for Distinct adjacent elements in an array problem

#include<bits/stdc++.h>
using namespace std;
void areDistinctAdjacent(int a[], int n)
{
    unordered_map<int, int> MAP;
    for (int i = 0; i < n; ++i)
        MAP[a[i]]++;
    int maxFreq = 0;
    for (int i = 0; i < n; ++i)
        if (maxFreq < MAP[a[i]])
            maxFreq = MAP[a[i]];
    if (maxFreq > (n + 1) / 2)
        cout << "NO";
    else
        cout << "YES";
}
int main()
{
    int arr[] = { 3,5,5,3,5 };
    int n = sizeof(arr) / sizeof(arr[0]);
    areDistinctAdjacent(arr, n);
    return 0;
}

 

YES

Java code for Distinct adjacent elements in an array problem

import java.util.HashMap;
import java.util.Map;

class adjacentDistinctElement
{
    static void areDistinctAdjacent(int a[], int n)
    {
        HashMap<Integer,Integer> MAP = new HashMap<Integer,Integer>();

        for (int i = 0; i < n; ++i)
        {
            if(MAP.containsKey(a[i]))
            {
                int x = MAP.get(a[i]) + 1;
                MAP.put(a[i],x);
            }
            else
            {
                MAP.put(a[i],1);
            }

        }
        int maxFreq = 0;

        for (int i = 0; i < n; ++i)
            if (maxFreq < MAP.get(a[i]))
                maxFreq = MAP.get(a[i]);

        if (maxFreq > (n + 1) / 2)
        {
            System.out.println("NO");
        }
        else
        {
            System.out.println("YES");
        }
    }
    public static void main (String[] args)
    {
        int arr[] = { 3,5,5,3,5 };
        int n = arr.length;
        areDistinctAdjacent(arr, n);
    }
}


YES

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. Because we have used Hashmap we are able to achieve linear time complexity.

Space Complexity

O(n) where “n” is the number of elements in the array. As we have used hashmap we were storing frequencies of elements. And in the worst case there may be all different elements. Then we’ll have N key-value pairs. So we have O(N) space complexity.

Translate »