Find minimum number of merge operations to make an array palindrome

Problem Statement

You are given an array of integers. The problem statement asks to find minimum number of merge operations to make an array palindrome, i.e. find out the minimum number of merging operations to be done on the array to make it a palindrome. Merging operation simply means that we can replace the sum of adjacent elements with the sum itself.

Example

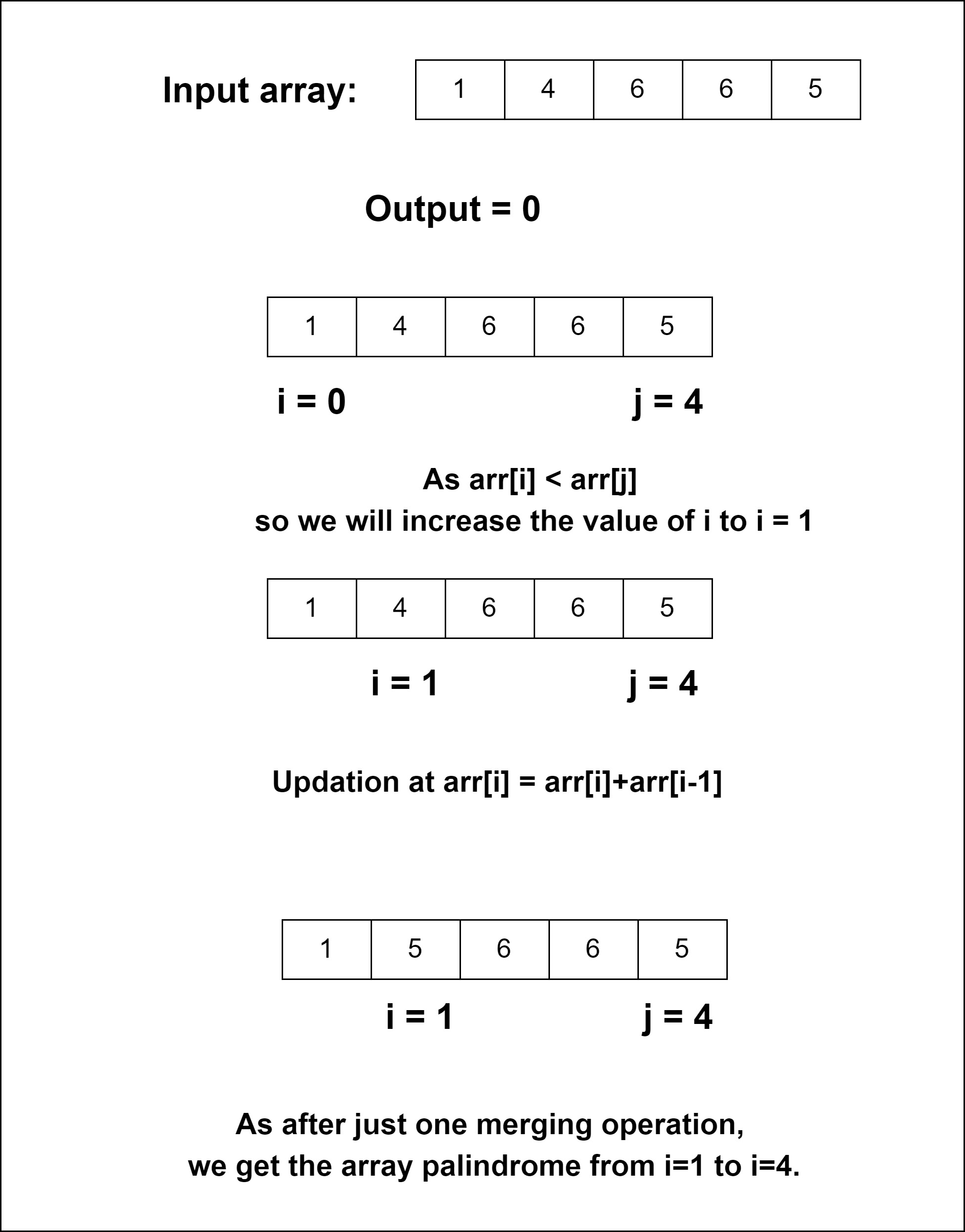
arr[] = {1, 4, 6, 6, 5}

1

Explanation: We can merge 1 and 4 with the sum of themselves, so it becomes 5 and our array becomes {5, 6, 6, 5}, which is a palindrome.

arr[] = {2,1,2,4,3}

2

Explanation: We can merge 1 and 2 with their sum, so it becomes 3 and also 2 and 4 can be merged, so our array becomes {3, 6, 3}

Algorithm to find minimum number of merge operations to make an array palindrome

1. Set the value of output to 0.
2. Traverse the array from i = 0 and j = n – 1, to i < n( length of an array).
  1. If arr[i] is equal to arr[j]
    1. Do i++ and j--.
  2. If arr[i] > arr[j]
    1. Do j—
    2. Update and restore the value of arr[j] = arr[j] + arr[j+1].
    3. Increase the output’s value by 1.
  3. If arr[i] < arr[j],
    1. Increase the value of i.
    2. Update arr[i] = arr[i] + arr[i-1].
    3. Increase the output’s value by 1.
3. Return output.

Explanation

We have given an array of integers. We are asked to find out the minimum number of merging operations that can be done onto the array to make it a palindrome array. Here merging means adding up two adjacent values and replaces them with their sum. Here we are going to find the number of operations to be done.

We are going to traverse the array from left and also from right making two pointers indicate the position of each traversal index. We chose both sides because we have to check if it is palindrome or not. And in palindrome from both sides according to their indexes elements are equal just like in string palindrome. So we will check the value of opposite sides and operate on their indexes. Then we perform merging operations and continue up till we find the count of merging operations to be done.

We will check if the first element from the left and from the right are equal. Then just shift the pointers towards the center one unit. Check for if the left pointer index element is greater than the right pointer index element, then decrease the value of the right pointer value and update the arr[j] with the sum of the adjacent elements and increase the value of output means our number of operations.

We will check for if the left pointer index element is smaller than the right pointer index element, then increase the value of the left pointer value and update the arr[i] with the sum of the adjacent elements and increase the value of output means our number of operations. And at last, we will return the output value.

Code to find minimum number of merge operations to make an array palindrome

C++ Code

#include<iostream>

using namespace std;

int getMinimumOperation(int arr[], int n)
{
    int output = 0;

    for (int i=0,j=n-1; i<=j;)
    {
        if (arr[i] == arr[j])
        {
            i++;
            j--;
        }
        else if (arr[i] > arr[j])
        {
            j--;
            arr[j] += arr[j+1] ;
            output++;
        }
        else
        {
            i++;
            arr[i] += arr[i-1];
            output++;
        }
    }
    return output;
}
int main()
{
    int arr[] = { 1, 4, 6, 6, 5};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << "Minimum operations to be done: "<< getMinimumOperation(arr, n);
    return 0;
}

Minimum operations to be done: 1

Java Code

class ArrayPalindromeMerging
{
    public static int getMinimumOperation(int[] arr, int n)
    {
        int output = 0;
        for (int i=0,j=n-1; i<=j;)
        {
            if (arr[i] == arr[j])
            {
                i++;
                j--;
            }
            else if (arr[i] > arr[j])
            {
                j--;
                arr[j] += arr[j+1] ;
                output++;
            }
            else
            {
                i++;
                arr[i] += arr[i-1];
                output++;
            }
        }
        return output;
    }
    public static void main(String[] args)
    {
        int arr[] = { 1, 4, 6, 6, 5} ;
        System.out.println("Minimum operations to be done : "+ getMinimumOperation(arr, arr.length));
    }
}

Minimum operations to be done : 1

Complexity Analysis

Time Complexity

We are simply traversing the array once, so this counts for linear time complexity. O(n) where “n” is the number of elements in the array.

Space Complexity

We are just using a single array having size n for storing the input, thus this algorithm for finding the number of merge operations to make an array palindrome has linear space complexity. O(n) where “n” is the number of elements in the array.