Find the minimum distance between two numbers

Difficulty Level Easy
Frequently asked in CouponDunia Coursera Delhivery Moonfrog Labs PayPal Paytm Snapchat
ArrayViews 2115

Problem Statement

You have given an array and two numbers called x and y. The problem “Find the minimum distance between two numbers” asks to find out the minimum possible distance between them. The array given can have common elements. You can assume that both x and y are different.

Example

arr[] = {1, 3, 2, 5, 8, 2, 5, 1}

x = 2

y=8
1

Explanation: Indices of 2 are 2 and 5 and the index of 8 is 4, so we take the index which computes the minimum distance between two given numbers.

arr[] = {1, 3, 2, 5, 8, 2, 5, 1}

x = 3

y=5
2

Explanation: Index of 3 is 1 and the index of 5 is 3. So the minimum distance between both of them is 3-1=2.

arr[] = {2, 4, 6, 8, 2, 5, 0, 56}

x = 6

y=5
3

Explanation: Index of 6 is 2 and the index of 5 is 5, so the minimum distance between both of them is 5-2=3.

Algorithm to find the minimum distance between two numbers

1. Set flag to -1 and output to the Maximum value of an Integer.
2. Traverse the array from i = 0 to i < n.
    1. Check if the array element is either equal to x or equal to y.
    2. Check if flag is not equal to i and arr[i] is not equal to arr[flag].
        1. If the condition is true, then find out the minimum between the output and i - flag.
3. Return output.

Explanation

We have given an array of integers and two integer numbers called x and y. We have to find out the minimum distance between the two given numbers, x, and y. To find out the minimum distance we will be checking two number pairs. The number which we are given, we will check only for them during the traversal. We will be searching for one of the two numbers, is matched with the array current element. If it is found to be true, then we will check if it is not the repeating element or the same element. If all of the conditions are found to be true, then we will just update the output value.

Any of the current array element is equal to either x or y, and another condition of indexes and the same elements has become false. Then we will just update the flag and store the current element index to flag. Let us consider an example and take a look at that:

Example

Arr[]={1, 3, 2, 5, 8, 2, 5, 1}, x = 2 , y=8

Output=Maximum value of an Integer, flag = – 1

We have given two numbers x = 2 and y = 8

  • i=0, we will check for if arr[i] is equal to 2 or arr[i] is equal to 8, but condition doesn’t satisfy.

The condition satisfies when i=2.

  • i=2, arr[i] is equal to 2.

We will check for the flag and it is false because the flag is still -1. So it will not enter in if, we will just update the flag as flag = 2.

  • Next pick, when i = 4, arr[i] = 8, flag is not equal to -1 and also arr[i] is not equal to arr[flag]. We are checking this condition so that we would not find the same number again and get its distance.

So now we will update the output as = 4 – 2 = 2. And also update flag = 4

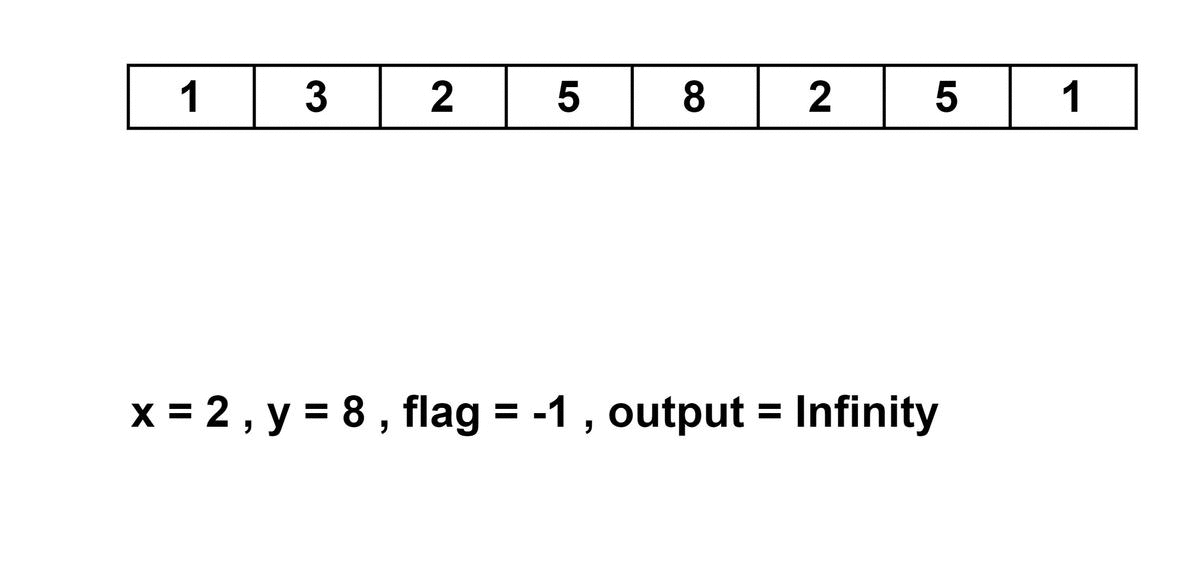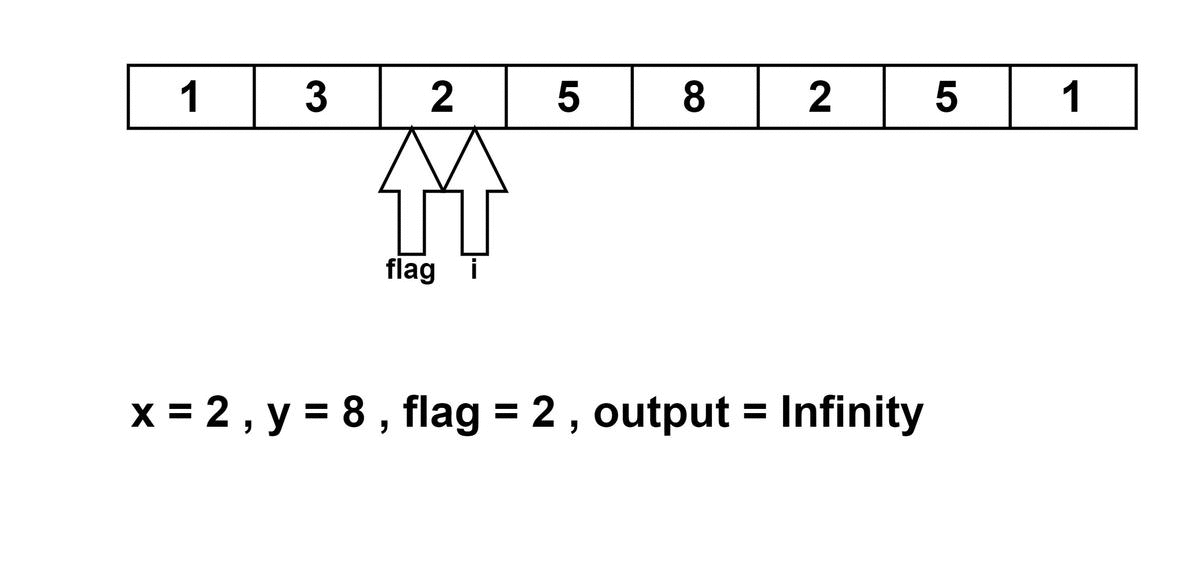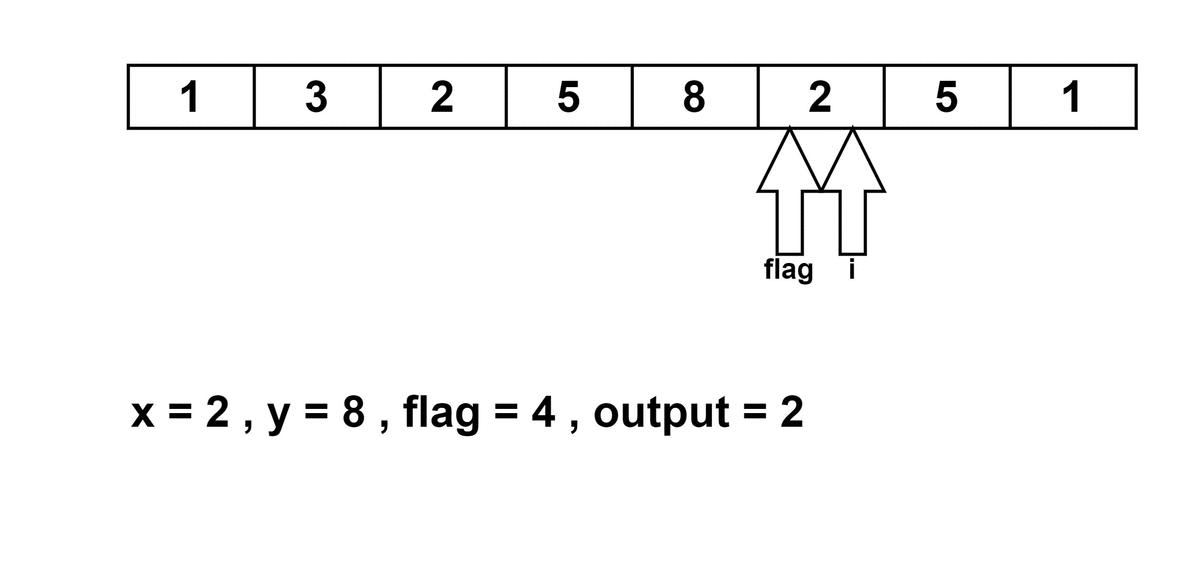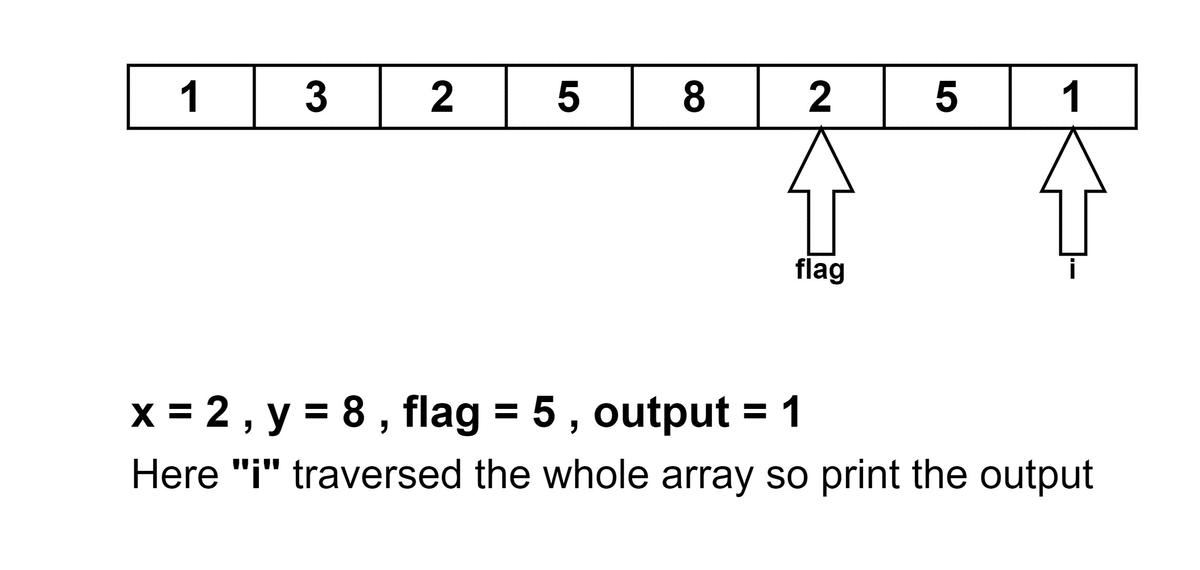
  • Again at i = 5, arr[i ] = 2, we will find the condition true, and also flag is not equal to -1 and arr[i] is not equal to arr [flag ], so we will update output again as the minimum between min(4, 5-4) and 1 will be updated in output.

So now we have the minimum distance as 1 between the array element arr[4] = 8 and arr[5] = 2.

Output = 1.

Find the minimum distance between two numbers

Code

C++ code to find the minimum distance between two numbers

#include<bits/stdc++.h>

using namespace std;

int getMinimumDistance(int arr[], int n, int x, int y)
{
    int flag=-1;
    int output=INT_MAX;

    for(int i = 0 ; i < n ; i++)
    {
        if(arr[i] ==x || arr[i] == y)
        {
            if(flag != -1 && arr[i] != arr[flag])
            {
                output = min(output,i-flag);
            }

            flag=i;
        }
    }
    if(output==INT_MAX)
        return -1;

    return output;
}

int main()
{
    int arr[] = {1, 3, 2, 5, 8, 2, 5, 1};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 2;
    int y = 8;

    cout << "Minimum possible distance between " << x <<" and " << y << " : "<<getMinimumDistance(arr, n, x, y);
    return 0;
}

Minimum possible distance between 2 and 8 : 1

Java code to find the minimum distance between two numbers

class MinimumDistanceBwNumbers
{
    public static int getMinimumDistance(int arr[], int n, int x, int y)
    {
        int flag=-1;
        int output=Integer.MAX_VALUE;

        for(int i = 0 ; i < n ; i++)
        {
            if(arr[i] ==x || arr[i] == y)
            {
                if(flag != -1 && arr[i] != arr[flag])
                {
                    output = Math.min(output,i-flag);
                }

                flag=i;
            }
        }
        if(output==Integer.MAX_VALUE)
            return -1;

        return output;
    }
    public static void main(String[] args)
    {
        int arr[] = {1, 3, 2, 5, 8, 2, 5, 1};
        int n = arr.length;
        int x = 2;
        int y = 8;

        System.out.println("Minimum possible distance between " + x + " and " + y + ": " + getMinimumDistance(arr, n, x, y));
    }
}

Minimum possible distance between 2 and 8: 1

Complexity Analysis

Time Complexity

Single traversal makes the algorithm run in linear time complexity. O(n) where “n” is the number of elements in the array.

Space Complexity

O(N) space complexity since we use an array to store the input. But the algorithm to find the minimum distance requires O(1) extra space.

Translate »