Find the smallest positive integer value that cannot be represented as sum of any subset of a given array

Problem Statement

You are given a sorted array of integers. We need to find the smallest positive integer value that cannot be represented as sum of any subset of a given array.

Example

arr[] = {1,4,7,8,10}

2

Explanation: Because there is not any sub-array that can represent 2 as a sum.

arr[] = {1,2,3,5,7,9}

28

Explanation: Because there is not any sub-array that can represent 28 as a sum.

Algorithm to find the smallest positive integer value that cannot be represented as sum of any subset of a given array

1. Set output to 1.
2. From i=0 to i less than n.
  1. Check if arr[i] is less than equal to output.
    1. Update the value of output to the sum of output and arr[i].
3. Return output.

Explanation

We are given a sorted array of integers. The problem statement asks to find the smallest positive integer value. That cannot be represented as sum of any subset of a given array. We can find this solution in linear time complexity O(n). As we have an array already sorted. So we need not worry about the order or number differences that’s why we will be able to find this in linear time.

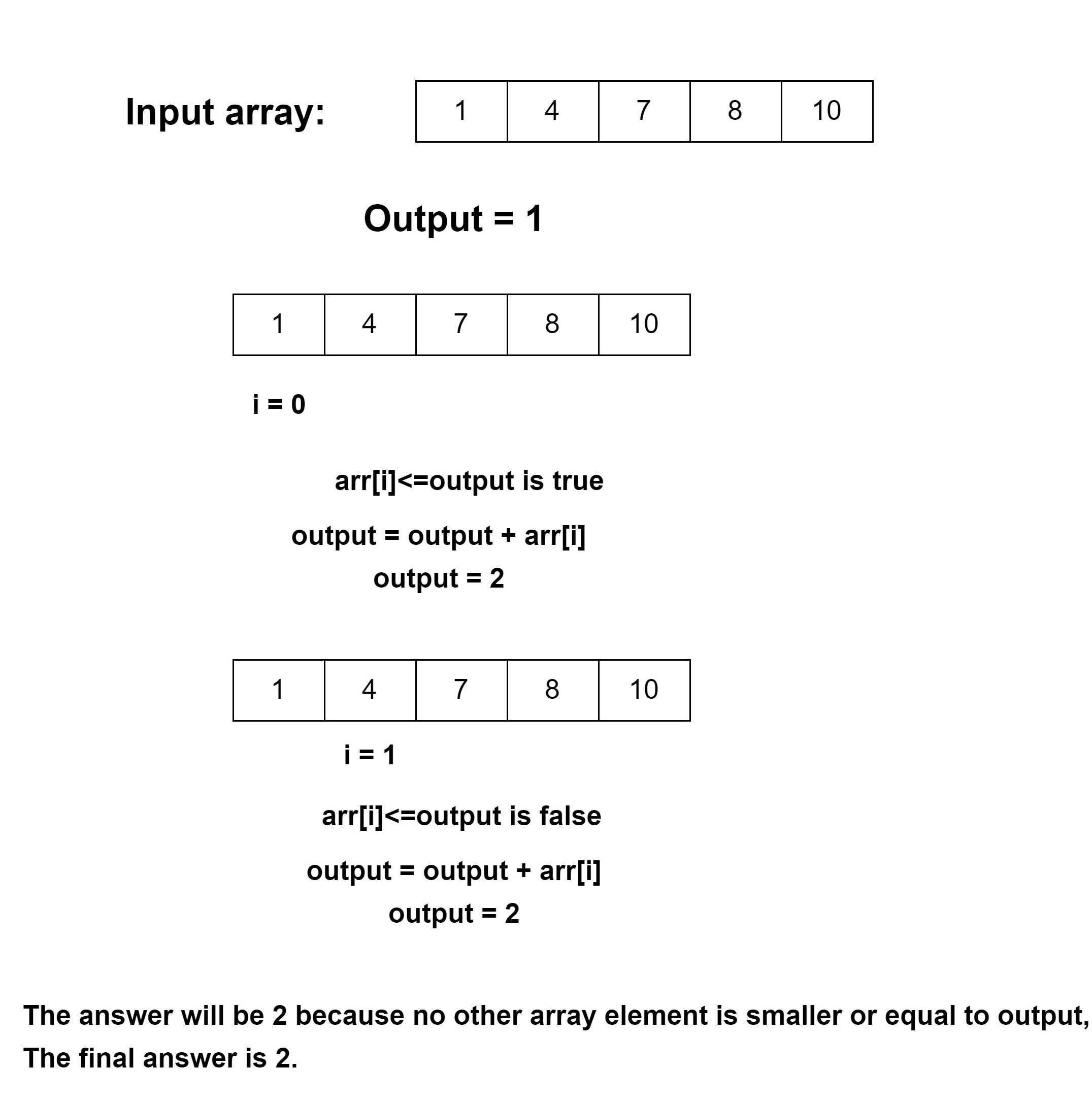
We are going to traverse the array. But before that set the value of output to 1, as at least there will be the smallest positive integer. If we do not have an array starting from 1, then simply it going to return 1 as an output value. So after setting up the output value as 1, traversing the array. We will pick up the first element of the array and check if it is smaller than or equal to the value of output. If it is true then we will be adding up the value of output and current array element. And then store this to output. We will keep doing this until the value of an array element will not go greater than the values of output. Then it will come out of the loop and we will return the value of output.

If we take an example as arr[]={1,4,7,8,10}, we will start with the output = 1, we will continue picking up the first element and check if it is less than or equal to output, it is true and we will go for adding up the value of output and arr[i] and store it to output and we have 2 now in output. Again we will be checking up for the values but now any value in the array is not equal or less than output, so finally 2 is our required answer and we going to return it.

Code to find the smallest positive integer value that cannot be represented as sum of any subset of a given array

C++ Code

#include<iostream>

using namespace std;

int getSmallestInteger(int arr[], int n)
{
    int output = 1;
    for (int i = 0; i < n && arr[i] <= output; i++)
        output = output + arr[i];

    return output;
}
int main()
{
    int arr[] = {1, 3, 4, 5};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout <<"Smallest positive integer : "<<getSmallestInteger(arr, n);

    return 0;
}

Smallest positive integer : 2

Java Code

class IntegernotSumofSubArray
{
    public static int getSmallestInteger (int arr[], int n)
    {
        int output = 1;

        for (int i = 0; i < n && arr[i] <= output; i++)
            output = output + arr[i];

        return output;
    }
    public static void main(String[] args)
    {
        int arr[] = {1, 3, 4, 5};
        int n = arr.length;
        System.out.println("Smallest positive integer : "+getSmallestInteger (arr, n));
    }
}

Smallest positive integer : 2

Complexity Analysis

Time Complexity for finding smallest positive number value that does not exist as subset sum in array

Whenever we simply traverse an array, we are doing an operation of linear time complexity. And since here we are doing nothing but single traversal, we have a linear time complexity. O(n) where “n”  is the number of elements in the array.

Space Complexity for finding smallest positive number value that does not exist as subset sum in array

We simply have a single array storing the input, thus algorithm has linear space complexity as well. O(n) where “n”  is the number of elements in the array.