In merge overlapping intervals problem we have given a collection of intervals, merge and return all overlapping intervals.
Table of Contents
Example
Input : [[2, 3], [3, 4], [5, 7]]
Output: [[2, 4], [5, 7]]
Explanation:
We can merge [2, 3] and [3, 4] together to form [2, 4]
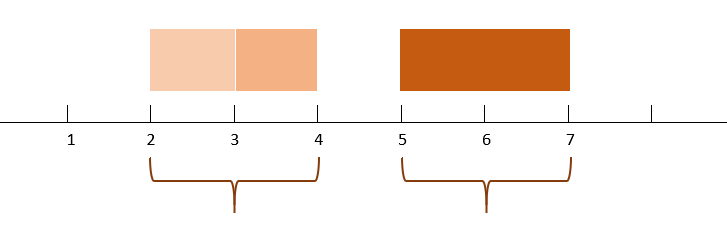
Approach for finding Merge Overlapping Intervals
The idea here is to sort the intervals based on the starting index so that we can merge them just by keeping a track of the start and end index for every merged interval.
If we have a merged interval [a, b] and the next interval is [c, d]. So there are three cases:
- When c<=d and d>=b then the resultant interval would be [a, d]
- And when c<=d and d<=b then the resultant interval would be [a, b]
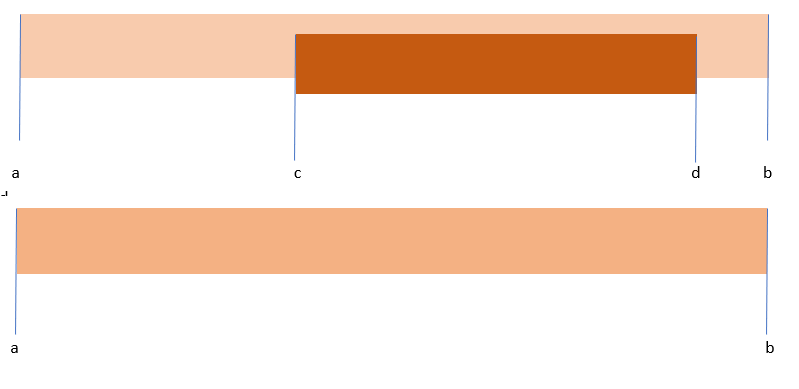
- When c>d, then the intervals can not be merged and we will have two resultant intervals [a, b] and [c, d]

Algorithm for finding Merge Overlapping Intervals
Step 1: Sort the intervals first based on their starting index and then based on their ending index. This step will take (nlogn) time.
Step 2: Initialize the starting and ending variable as -1, this indicates that currently there is no interval picked up.
Step 3: Iterate over the interval array and check these three conditions:
- If the starting and ending variable is -1, then pick the ith interval and update the starting and ending variable.
- Now check If the ith interval overlaps with the previously picked interval then modify the ending variable with the maximum of the previous ending and the end of the ith interval.
- If the ith interval does not overlap with the previously picked interval then push the previous interval in the ans array and update the starting and ending variable with the ith interval.
Implementation
C++ program Merge Overlapping Intervals
#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
vector<vector<int>> ans;
int i=0;
int n=intervals.size(),s=-1,e=-1;
while(i<n){
if(s==-1){
s=intervals[i][0];
e=intervals[i][1];
i++;
}
else{
if(intervals[i][0]<=e){
e=max(e,intervals[i][1]);
i++;
}
else{
ans.push_back(vector<int>{s, e});
s=intervals[i][0];
e=intervals[i][1];
i++;
}
}
}
if(s!=-1){
ans.push_back(vector<int>{s, e});
}
return ans;
}
int main(){
int n;
cin>>n;
vector<vector<int>> intervals(n);
for(int i=0;i<n;i++){
int a,b;
cin>>a>>b;
intervals[i].push_back(a);
intervals[i].push_back(b);
}
vector<vector<int>> ans = merge(intervals);
cout<<"Intervals after merge operation are:\n";
for(int i=0;i<ans.size();i++){
cout<<ans[i][0]<<" "<<ans[i][1]<<"\n";
}
}
4 1 3 2 6 8 10 15 18
Intervals after merge operation are: 1 6 8 10 15 18
JAVA program for Merge Overlapping Intervals
import java.util.*;
public class Main
{
public static int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (a,b)->Integer.compare(a[0],b[0]));
ArrayList<int[]> list = new ArrayList();
int i=0;
int n=intervals.length,s=-1,e=-1;
while(i<n){
if(s==-1){
s=intervals[i][0];
e=intervals[i][1];
i++;
}
else{
if(intervals[i][0]<=e){
e=Math.max(e,intervals[i][1]);
i++;
}
else{
list.add(new int[]{s, e});
s=intervals[i][0];
e=intervals[i][1];
i++;
}
}
}
if(s!=-1){
list.add(new int[]{s, e});
}
int[][] arr = new int[list.size()][2];
return list.toArray(arr);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] arr = new int[n][2];
for(int i=0;i<n;i++){
arr[i][0] = sc.nextInt();
arr[i][1] = sc.nextInt();
}
int[][] ans = merge(arr);
System.out.println("Intervals after merge operation are:");
for(int i=0;i<ans.length;i++){
System.out.println(ans[i][0]+" "+ans[i][1]);
}
}
}
5 1 2 2 5 2 6 7 9 15 18
Intervals after merge operation are: 1 6 7 9 15 18
Complexity Analysis
Time Complexity
O(nlogn)
Sorting takes O(nlogn) time and traversal of the array for once takes O(n) time.
Hence to total time complexity is O(nlogn + n) i.e., O(nlogn)
Space Complexity
O(n) because we use a vector to store the result and its maximum size is N when all the intervals are overlapped.