Move all negative elements to end in order with extra space allowed

Problem Statement

“Move all negative elements to end in order with extra space allowed” states that you are given an array containing positive and negative numbers both. The problem statement asks to move all the negative elements in the last of the array.

Example

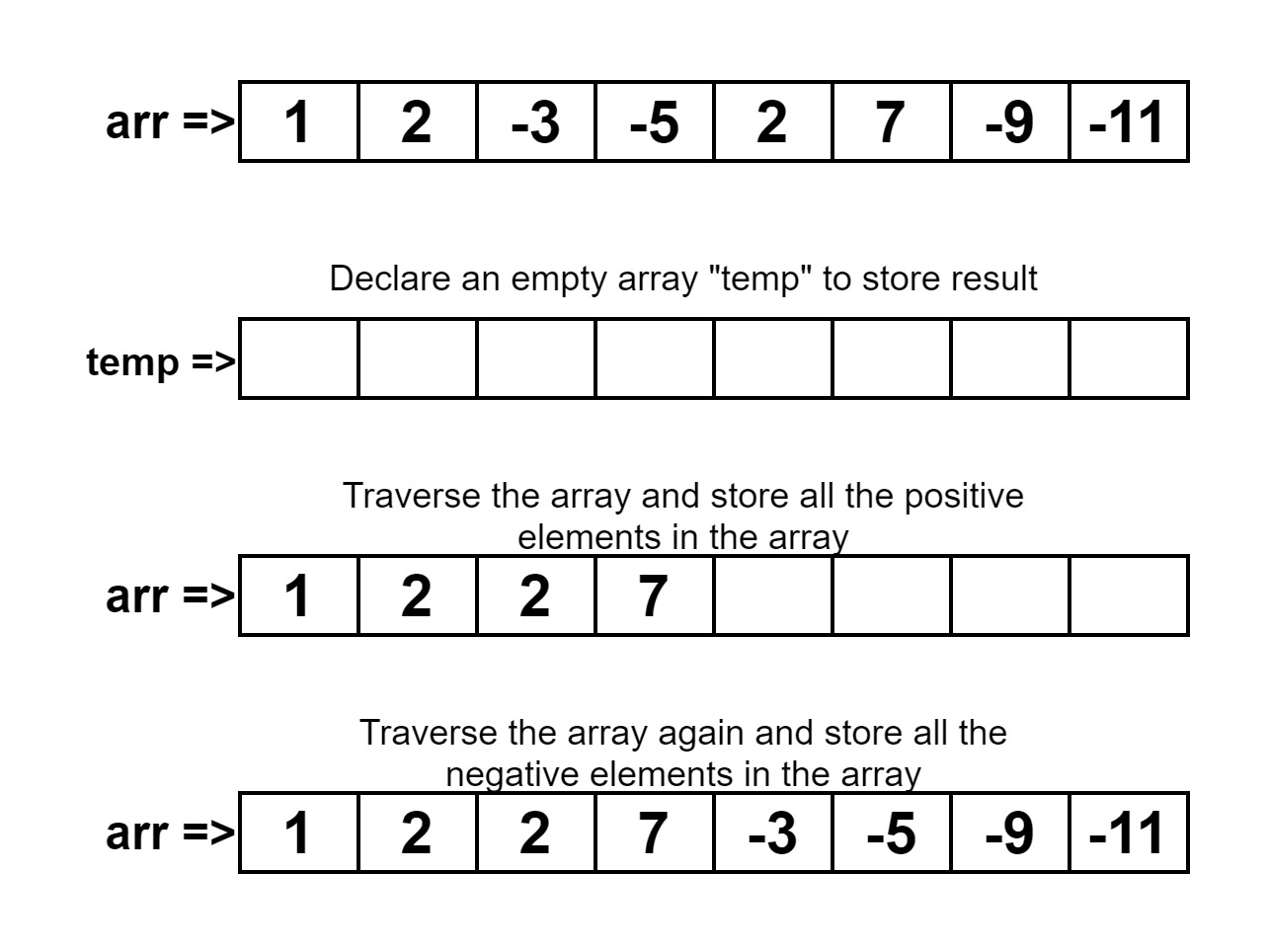
arr[] = { 1,2,-3,-5,2,7,-9,-11 }

1, 2, 2, 7, -3, -5, -9, -11

Algorithm to Move all negative elements to end in order with extra space allowed

1. Declare an array same as the size of the original array.
2. Traverse the array and check if any number is greater than or equal to 0,
    1. If true then copy that number from the 0th position of the array we created.
3. Now traverse the array and check if any of the numbers is less than 0.
    1. If true, then copy that value to the array we created from the next position where the positive number ends.
4. Now copy that temporary array we created into the original array and print that array.

Explanation

We are given an integer array containing both negative and positive numbers. We have asked to rearrange the array in such a manner that we have to move all the negative elements to the last/end of the array. Then we will be traversing the array for positive and negative elements separately. First, we have to perform operations on positive elements where we have to pull them to the left. And then shift all the negative elements to the right.

We have to create an extra array of the same size as that of the original array. Because in this, we will be storing the desired arrangement of numbers. Picking up a variable index and initialize it as 0. This variable will help us to distinguish between the positive and negative elements. Now we created an array. We will be putting in the positive numbers from the original array to the temporary array.

We will check while traversing if the array elements are greater than or equal to 0, then only copy that element into the temporary array, from the starting position of temporary array. Also, we are increasing out index value simultaneously, so since we last copy the positive element we have a value index as of next element where it to be stored, with the help of this we will be pushing all the negative elements at the last.

Now we will go for traversing the array again and checking if each of the elements is less than the 0 if it is zero then start pushing that value into the temporary array from the index value where we left off. At last, copy that array to the original array then print it or simply the printing the temporary array, both are the same things. And we get the required output.

Code

C++ code to Move all negative elements to end in order with extra space allowed

#include<bits/stdc++.h>
using namespace std;

void segregateElements(int arr[], int n)
{
    int temp[n];

    int j = 0;

    for (int i = 0; i < n ; i++)
        if (arr[i] >= 0 )
            temp[j++] = arr[i];

    if (j == n || j == 0)
        return;

    for (int i = 0 ; i < n ; i++)
        if (arr[i] < 0)
            temp[j++] = arr[i];

    memcpy(arr, temp, sizeof(temp));
}

void printArray(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
}

int main()
{
    int arr[] = { 1,2,-3,-5,2,7,-9,-11 };
    int n = sizeof(arr)/sizeof(arr[0]);

    segregateElements(arr, n);
    printArray(arr,n);

    return 0;
}

1 2 2 7 -3 -5 -9 -11

Java code to Move all negative elements to end in order with extra space allowed

import java.util.Arrays;

class moveNegativeElement
{
    public static void segregateElements(int arr[], int n)
    {
        int temp[] = new int[n];

        int j = 0;

        for (int i = 0; i < n; i++)
            if (arr[i] >= 0)
                temp[j++] = arr[i];

        if (j == n || j == 0)
            return;

        for (int i = 0; i < n; i++)
            if (arr[i] < 0)
                temp[j++] = arr[i];

        for (int i = 0; i < n; i++)
            arr[i] = temp[i];
    }
    public static void printArray(int arr[], int n)
    {
        for (int i = 0; i < n; i++)
            System.out.print(arr[i] + " ");
    }
    public static void main(String arg[])
    {
        int arr[] = { 1,2,-3,-5,2,7,-9,-11 };
        int n = arr.length;

        segregateElements(arr, n);
        printArray(arr,n);

    }
}

1 2 2 7 -3 -5 -9 -11

Complexity Analysis

Time Complexity

O(N) where “N” is the of elements in the array. We have simply just traversed the array due to which we have achieved linear time complexity.

Space Complexity

O(N) where “N” is the of elements in the array. We have created an extra array for temporary use where we have stored the elements in the desired manner.