Replace two consecutive equal values with one greater

Difficulty Level Easy
Frequently asked in Accenture Citadel FreeCharge PayPal Square Teradata
ArrayViews 2351

Problem Statement

Suppose you have an integer array. The problem “Replace two consecutive equal values with one greater” asks to replace all those pair values say ‘a’ which comes consecutively with a number “a+1” 1 greater than them (two consecutive numbers), such that even after the modification or repetition there will be no new consecutive pair remaining.

Example

arr[]={5, 2, 1, 1, 2, 2}
5 4

Explanation

As 1 is a consecutive number it is replaced by a value greater than that means 2 and arr will become {5,2,2,2,2}

Now 2 is a consecutive number so will be replaced by a number greater than it i.e., 3 and arr will become {5,3,2,2}

Again 2 is a consecutive number so will be replaced by 3 and arr will become {5,3,3}

Now 3 is the consecutive number so will be replaced by 4 and arr will become {5,4}

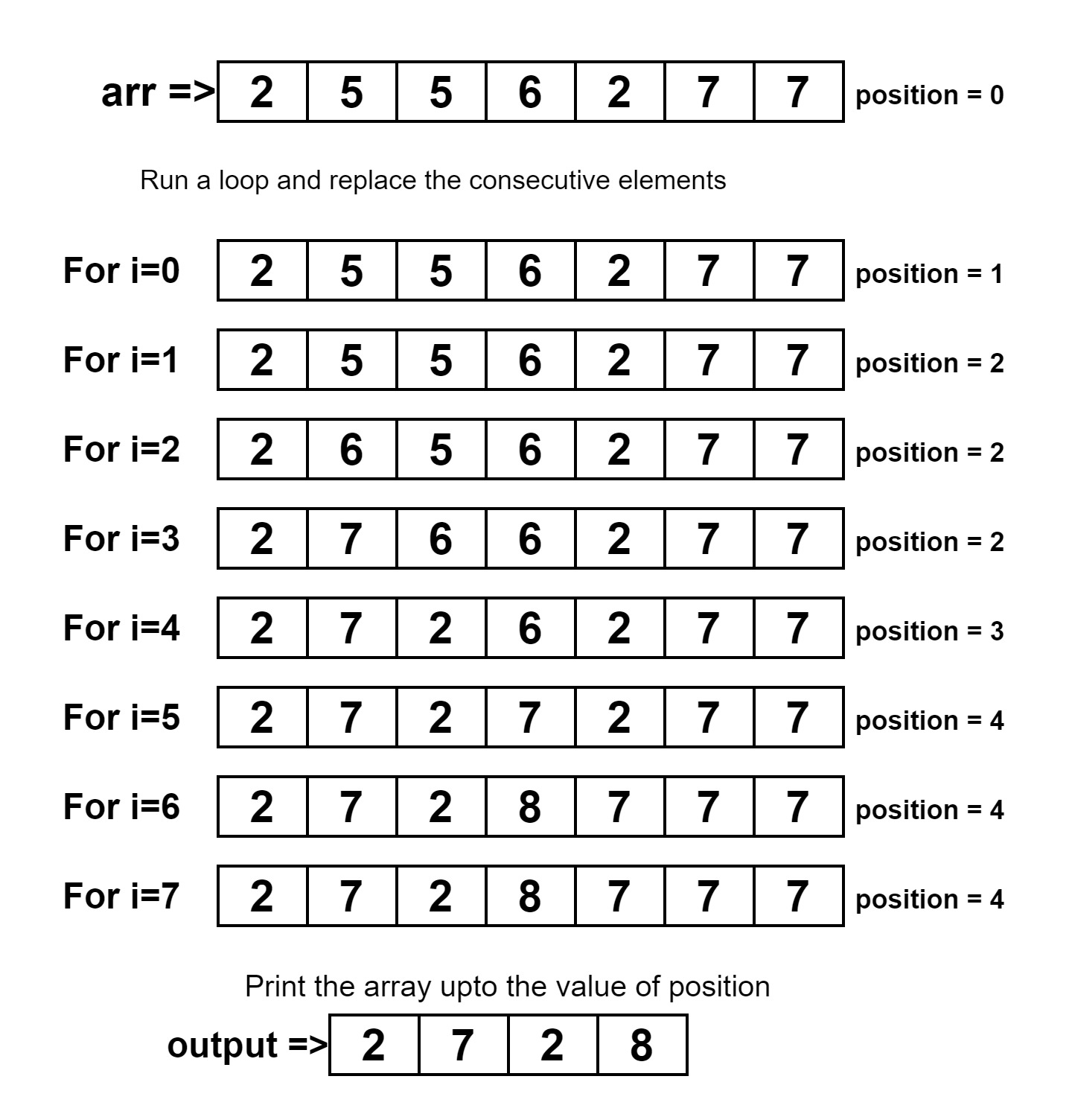
arr[]={2,5,5,6,2,7,7}
2 7 2 8

Explanation

As 5 is a consecutive number it is replaced with a value 1 greater than that means 6. So arr will look like arr[]={2,6,6,2,7,7}

6 come in place of that but the next number is also 6, so it is also replaced with the value 1 greater than 6, means 7 and arr will become {2,7,2,7,7}

As 7 also occurs consecutively at last, so it is replaced with the 8 and arr will become {2,7,2,8}

Algorithm

1. Set the position’s value to 0.
2. Traverse the array from o to n(n is the length of the array).
  1. Copy the value of arr[i] to arr[position] and increase the value of the position by 1.
  2. While the position is greater than 1, its previous two values are equal or not.
    1. Decrease the value of a position by 1,
    2. and increase the value of arr[position -1] by 1.
3. Print the array from index 0 to position.

Explanation

We have given an array of integers. We have asked to replace all those values which come consecutively with a number 1 greater than the number itself. If 4 come in arrays consecutively, then it will be replaced with the value 5. That is 1 greater than the number 4. Now with one traversal, we can only make a modification. Suppose, there are 3 numbers present 4, 4, 5. Then we will be converting 4, 4 to 5 and then also 5 is a consecutive number. Because its next number is same as the number itself. So we will be doing this using a nested loop.

Traverse the array from 0 to n. Open a loop, so it will become a nested loop. With the outer loop, we will be handling the traversals. And with the inner loop, we are going to update the values or replace the values according to the given condition. In the outer loop, we are going to copy the values in the same array up to two values.

Only after two traversals in the outer loop, it will go in the inner loop. In a while loop, we are going to check if the indices value is greater than 1. Because we are going to compare if the previous two values are equal. That’s why we leave that condition that two values must be copied into the array positioned values. Then simply decrease the values of position and update the array element with values 1 greater than the number itself. We will just keep on with this loop and this method. It will continuously replace all those values with the consecutive ones.

Now print the array from 0 to index position which was last updated, it will give the desired array.

Replace two consecutive equal values with one greater

 

Code

C++ code to Replace two consecutive equal values with one greater

#include<iostream>

using namespace std;

void replaceValues(int arr[], int n)
{
    int position = 0;

    for (int i = 0; i < n; i++)
    {
        arr[position++] = arr[i];
        while (position > 1 && arr[position - 2] == arr[position - 1])
        {
            position--;
            arr[position - 1]++;
        }
    }
    for (int i = 0; i < position; i++)
        cout << arr[i] << " ";
}
int main()
{
    int arr[] = { 2,5,5,6,2,7,7};
    int n = sizeof(arr) / sizeof(int);
    replaceValues(arr, n);
    return 0;
}

2 7 2 8

Java code to Replace two consecutive equal values with one greater

class replaceConsecutiveValues
{
    public static void replaceValues(int arr[], int n)
    {
        int position = 0;
        for (int i = 0; i < n; i++)
        {
            arr[position++] = arr[i];
            while (position > 1 && arr[position - 2] == arr[position - 1])
            {
                position--;
                arr[position - 1]++;
            }
        }
        for (int i = 0; i < position; i++)
            System.out.print( arr[i] + " ");
    }
    public static void main(String args[])
    {
        int arr[] = {2,5,5,6,2,7,7};
        int n = arr.length;
        replaceValues (arr, n);
    }
}

2 7 2 8

Complexity Analysis

Time Complexity

O(n2) where“n” is the number of elements in the array. Because we have used two nested loops which made the algorithm to run in polynomial time.

Space Complexity

O(1), that is independent of the number of elements in the array. The algorithm itself takes constant space but the program as a whole takes O(N) space(for input).

Translate »