In the Search Insert Position problem, we have given an integer x and a sorted array a[ ] of size n. Find the appropriate index or position at which the given integer must be inserted if given integer, not in the array. If given integer present in the input array then we print the index at which it present.
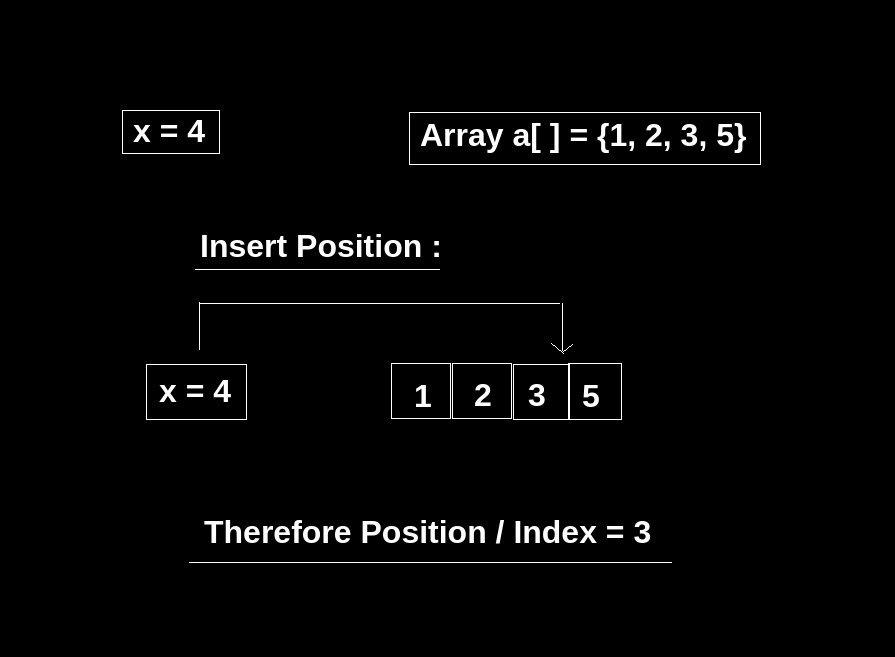

Table of Contents
Example
Input
x = 4
a[ ] = {1, 2, 3, 5}
Output
3
Input
x = 2
a[ ] = {1, 3, 4, 5}
Output
1
Input
x = 1
a[ ] = {3, 4, 5, 10}
Output
0
Using Linear Search
Algorithm
- Initialize an integer x and a sorted array of size n.
- Start traversing the given sorted array from 0 to n-1.
- Check if the element at the current index is equal to the given integer return the current index.
- Check if the element at the current index is greater than the given integer return the current index.
- If all the elements in the array are smaller than the given integer return n.
C++ Program to search insert position
#include <iostream>
using namespace std;
int insert(int x, int a[], int n){
for(int i=0; i<n; i++){
if(a[i]==x){
return i;
}
if(a[i]>x){
return i;
}
}
return n;
}
int main(){
int x = 4;
int a[] = {1, 2, 3, 5};
int n = sizeof(a)/sizeof(a[0]);
cout<<insert(x, a, n);
return 0;
}3
Java Program to search insert position
class InsertPosition{
static int insert(int x, int a[], int n){
for(int i=0; i<n; i++){
if(a[i]==x){
return i;
}
if(a[i]>x){
return i;
}
}
return n;
}
public static void main (String[] args){
int x = 4;
int a[] = {1, 2, 3, 5};
int n = a.length;
System.out.println(insert(x, a, n));
}
}3
Time Complexity
O(n) where n is the number of elements present in the given array. Here we visit all the index of the array which takes linear time.
Auxiliary Space
O(1) because we don’t use any auxiliary space to perform the operations.
Using Binary Search
Algorithm
- Initialize an integer x and a sorted array of size n.
- If a given integer is less than the first element of array return 0.
- Initialise beg =0, end = n-1 and mid as beg+end /2 .
- Traverse to check if the element is present in the array or not. Check if the element at mid is equal to the given element return current index.
- Else make a recursive call to the binary search function with an updated ending or starting index.
- If element is found in array return it’s index.
- Else traverse while beg is less than equal to end.
- If the element at mid is less than equal to x check if the element at mid+1 is greater than equal to x return mid +1 else update beg as mid+1 and mid as (beg+end)/2.
- Else if the element at mid is greater than equal to x check if the element at mid-1 is less than equal to x return mid -1 else update end as mid-1 and mid as (beg+end)/2.
- If all the elements in the array are smaller than the given integer return n.
C++ Program to search insert position
#include <iostream>
using namespace std;
int binarys(int arr[], int l, int r, int x){
if(r >= l){
int mid = l + (r - l) / 2;
if(arr[mid] == x)
return mid;
if(arr[mid] > x)
return binarys(arr, l, mid - 1, x);
return binarys(arr, mid + 1, r, x);
}
return -1;
}
int insert(int x, int a[], int n){
int beg = 0, end = n-1;
int mid = (beg+end)/2;
if(x<a[0]){
return 0;
}
int res = binarys(a, beg, end, x);
if(res!=-1){
return res;
}
while(beg<=end){
if(a[mid]<=x){
if(a[mid+1]>=x){
return mid+1;
}
else{
beg = mid+1;
mid = (beg+end)/2;
}
}
if(a[mid]>=x){
if(a[mid-1]<=x){
return mid-1;
}
else{
end = mid-1;
mid = (beg+end)/2;
}
}
}
return n;
}
int main(){
int x = 4;
int a[] = {1, 2, 3, 5};
int n = sizeof(a)/sizeof(a[0]);
cout<<insert(x, a, n);
return 0;
}3
Java Program to search insert position
class InsertPosition{
static int binarys(int[] arr, int l, int r, int x){
if(r >= l){
int mid = l + (r - l) / 2;
if(arr[mid] == x)
return mid;
if(arr[mid] > x)
return binarys(arr, l, mid - 1, x);
return binarys(arr, mid + 1, r, x);
}
return -1;
}
static int insert(int x, int a[], int n){
int beg = 0, end = n-1;
int mid = (beg+end)/2;
if(x<a[0]){
return 0;
}
int res = binarys(a, beg, end, x);
if(res!=-1){
return res;
}
while(beg<=end){
if(a[mid]<=x){
if(a[mid+1]>=x){
return mid+1;
}
else{
beg = mid+1;
mid = (beg+end)/2;
}
}
if(a[mid]>=x){
if(a[mid-1]<=x){
return mid-1;
}
else{
end = mid-1;
mid = (beg+end)/2;
}
}
}
return n;
}
public static void main (String[] args){
int x = 4;
int a[] = {1, 2, 3, 5};
int n = a.length;
System.out.println(insert(x, a, n));
}
}3
Time Complexity
O(log n) because we apply the concept of the binary search. We know that binary search takes logN time to find any number in the sorted array.
Auxiliary Space
O(1) because we don’t use any auxiliary space to perform the operations.