Table of Contents
Problem
In the Valid Triangle Number problem, we have given an array of non-negative integers. Find the number of triplets that can form a triangle. If we consider the numbers in the array as side lengths of the triangle.
Example
Input
[ 2, 2, 3, 4 ]
Output
3
Explanation
We can form three triplets that can form a triangle.
triplets are :
- 2,3,4 (using the first 2)
- 2,3,4 (using the second 2)
- 2,2,3
Brute force approach
A triplet can form a triangle if and only if it satisfies the condition a+b>c. It means that sum of two sides of a triangle must be greater than the third side.
The brute force approach is very simple and easy. We will check for each triplet if they satisfy the condition to form a triangle. We will also maintain a variable to keep track of the count of triplets that can form a triangle. So when we encounter a triplet that can form a triangle we will increase the count. In this way, after checking for all the possible triplets we will have the total number of triplets that can be formed.
Implementation of Valid Triangle Number
C++ code for Valid Triangle Number
// C++ code to count the number of
// possible triangles using brute
// force approach
#include <bits/stdc++.h>
using namespace std;
// Function to count all possible
// triangles with arr[] elements
int findNumberOfTriangles(int arr[], int n)
{
// Count of triangles
int count = 0;
// The three loops select three
// different values from array
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// The innermost loop checks for
// the triangle property
for (int k = j + 1; k < n; k++)
// Sum of two sides is greater
// than the third
if (
arr[i] + arr[j] > arr[k]
&& arr[i] + arr[k] > arr[j]
&& arr[k] + arr[j] > arr[i])
count++;
}
}
return count;
}
// Driver code
int main()
{
int arr[] = { 10, 21, 22, 100, 101, 200, 300 };
int size = sizeof(arr) / sizeof(arr[0]);
cout
<< "Total number of triangles possible is "
<< findNumberOfTriangles(arr, size);
return 0;
}
Total number of triangles possible is 6
Java code for Valid Triangle Number
// Java code to count the number of
// possible triangles using brute
// force approach
import java.io.*;
import java.util.*;
class check
{
// Function to count all possible
// triangles with arr[] elements
static int findNumberOfTriangles(int arr[], int n)
{
// Count of triangles
int count = 0;
// The three loops select three
// different values from array
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// The innermost loop checks for
// the triangle property
for (int k = j + 1; k < n; k++)
// Sum of two sides is greater
// than the third
if (
arr[i] + arr[j] > arr[k]
&& arr[i] + arr[k] > arr[j]
&& arr[k] + arr[j] > arr[i])
count++;
}
}
return count;
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 10, 21, 22, 100, 101, 200, 300 };
int size = arr.length;
System.out.println( "Total number of triangles possible is "+
findNumberOfTriangles(arr, size));
}
}Total number of triangles possible is 6
Time complexity
O(n^3) Because we are using three loops to find the triplet.
Space complexity
O(1) Because we are maintaining the count variable to keep track of triplets that can form triangles.
Efficient Approach
To optimize the solution we sort the array. We will run two loops.
- The first loop will keep track of the first side and the second loop will keep track of the second side of the triangle.
- The first loop runs from start to end and the second loop runs from i+1 to end.
- We will maintain a variable k =i+2;
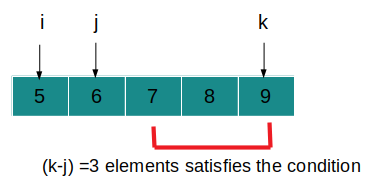
- After fixing the first and second sides we need the third side such that a+b>c. We will find a position(k) where the value of c is the maximum possible satisfying the condition to form a triangle.
- Then we will add ( k-j ) to the total count.
Implementation of Valid Triangle Number
C++ Program for Valid Triangle Number
// C++ program to count number of triangles that can be
// formed from given array
#include <bits/stdc++.h>
using namespace std;
int comp(const void* a, const void* b)
{
return *(int*)a > *(int*)b;
}
int findNumberOfTriangles(int arr[], int n)
{
// Sort the array elements in non-decreasing order
qsort(arr, n, sizeof(arr[0]), comp);
// Initialize count of triangles
int count = 0;
for (int i = 0; i < n - 2; ++i) {
// Initialize index of the rightmost third
// element
int k = i + 2;
// Fix the second element
for (int j = i + 1; j < n; ++j) {
while (k < n && arr[i] + arr[j] > arr[k])
++k;
if (k > j)
count += k - j - 1;
}
}
return count;
}
// Driver code
int main()
{
int arr[] = { 10, 21, 22, 100, 101, 200, 300 };
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Total number of triangles possible is " << findNumberOfTriangles(arr, size);
return 0;
}
Total number of triangles possible is 6
Java Program for Valid Triangle Number
// Java program to count number of triangles that can be
// formed from given array
import java.io.*;
import java.util.*;
class CountTriangles {
// Function to count all possible triangles with arr[]
// elements
static int findNumberOfTriangles(int arr[])
{
int n = arr.length;
// Sort the array elements in non-decreasing order
Arrays.sort(arr);
// Initialize count of triangles
int count = 0;
for (int i = 0; i < n - 2; ++i) {
// Initialize index of the rightmost third element
int k = i + 2;
// Fix the second element
for (int j = i + 1; j < n; ++j) {
while (k < n && arr[i] + arr[j] > arr[k])
++k;
if (k > j)
count += k - j - 1;
}
}
return count;
}
public static void main(String[] args)
{
int arr[] = { 10, 21, 22, 100, 101, 200, 300 };
System.out.println("Total number of triangles is " + findNumberOfTriangles(arr));
}
}Total number of triangles possible is 6
Time complexity
O(n^2)
Because we are using two loops to find the triplet.
Space complexity
O(1) Because we are maintaining the count variable to keep track of triplets that can form triangles.