Constant time range add operation on an array

You have given an integer array and initially, it was initialized as 0 and also given a range. The task is to add the given number in the range of the array and print the resultant array.

Example

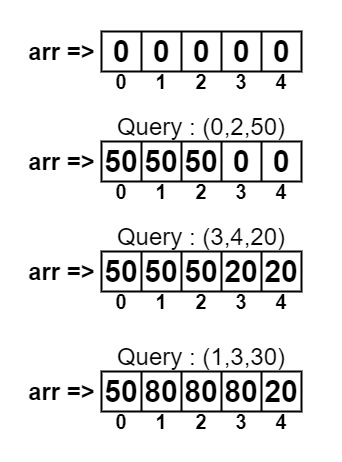
arr[] = {0, 0, 0, 0, 0}

Query: {(0, 2, 50), (3, 4, 20), (1, 3, 30)}

50 80 80 50 20

Explanation

50 is added to 0 to 2 in the array, array will become ⇒ {50, 50, 50, 0, 0}

20 is added to 3 to 4 in the array, array will become ⇒ {50, 50, 50, 20, 20}

30 is added to 1 to 3 in the array, array will become ⇒ {50, 80, 80, 80, 20}

Algorithm

1. For each query of the range follow the steps.
   1. Add the given value at the left index of the array and store it to itself.
   2. Check if the value right is not equal to the last array index, then subtract the given value at the right + 1 position of the array and store it to itself.
2. Before printing the array update the array as traverse through the array and add the previous and the current value and store it to the array value itself.
3. After updation, print the resultant array.

Explanation for Constant time range add operation on an array

Given an integer array and the number to add. We are also given a range of the query. It contains the starting point of the range as left and the ending point of the range as right. We have been asked to add the given number in the given range to all the possible integers. And then finally print the resultant array. For this, we are going to perform the addition operation in a very modified way. We will fill up the array index values with the given value at the left and right+1 position of the array and before printing update that array.

For each given query, left and right, we are going to add the given value at the left index of the right, remember only at left index. And for the right value, we are going to check if the value right is not equal to the last index of the array, if the given condition satisfied then we are going to update the given value index, we will subtract the given value from the right index of the array and store it to the right position index of the array itself. For each and every query, we are going to perform these operations.

Now we have to print the array, but before that, we are going to update all the value, the addition operation we have performed, we need to update that. So update the array, by traversing the array and adding up the current value and the previous value of the given array and store it to the current position of the array. Then after, we are going to print the array.

Code

Implementation in C++ for Constant time range add operation on an array

#include<iostream>

using namespace std;

void update(int arr[], int N)
{
    for (int i = 1; i < N; i++)
        arr[i] += arr[i - 1];
}

void addOperation(int arr[], int N, int left, int right, int value)
{
    arr[left] += value;
    if (right != N - 1)
        arr[right + 1] -= value;
}

void printArray(int arr[], int N)
{
    update(arr, N);
    for (int i = 0; i < N; i++)
        cout << arr[i] << " ";
    cout << endl;
}

int main()
{
    int N = 5;

    int arr[N] = {0};

    addOperation(arr, N, 0, 2, 50);
    addOperation(arr, N, 3, 4, 20);
    addOperation(arr, N, 1, 3, 30);

    printArray(arr, N);
    return 0;
}

50 80 80 50 20

Implementation in Java for Constant time range add operation on an array

class AddOperation
{
    static void update(int arr[], int N)
    {
        for (int i = 1; i < N; i++)
            arr[i] += arr[i - 1];
    }
    static void addOperation(int arr[], int N, int left, int right, int value)
    {
        arr[left] += value;
        if (right != N - 1)
            arr[right + 1] -= value;
    }
    static void printArray(int arr[], int N)
    {
        update(arr, N);

        for (int i = 0; i < N; i++)
            System.out.print(""+arr[i]+" ");
        System.out.print("\n");
    }
    public static void main (String[] args)
    {
        int N = 5;

        int arr[] = new int[N];

        addOperation(arr, N, 0, 2, 50);
        addOperation(arr, N, 3, 4, 20);
        addOperation(arr, N, 1, 3, 30);
        printArray(arr, N);
    }
}

50 80 80 50 20

Complexity Analysis

Time Complexity

O(N + Q) where “N” is the number of elements in the array and “Q” is the number of queries. Because we have incremented the value at left index and decremented the value at the right+1 index if it exists in the boundary of the array.

Space Complexity

O(N) where “N” is the number of elements in the array.