Find whether a subarray is in form of a mountain or not

Problem Statement

The problem “Find whether a subarray is in form of a mountain or not” states that you are given an integer array and a range. The problem statement asks to find out whether the sub-array formed between the given range is in form of a mountain form or not? Mountain array is formed if the numbers are in increasing order or in decreasing order or first increasing then decreasing.

Example

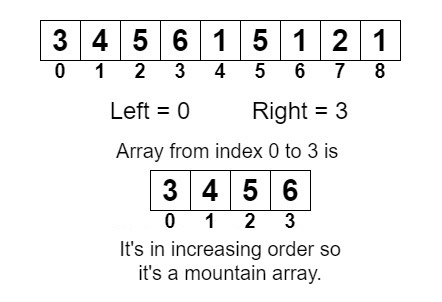
arr[]={3,4,5,6,1,5,1,2,1}

Left, right = (0, 3)

Mountain Form

Explanation

Because the sub-array {3, 4, 5, 6} is increasing, so it is in form of the mountain array.

arr[]={3,4,5,6,1,5,1,2,1}

Left, right = (5, 7)

Not a Mountain form

Explanation

Because the sub array {5, 1, 2} is decreasing then increasing. So it is not in the form of a mountain array.

Algorithm

1. Create two arrays arrayL and arrayR of same size as that of the length of original array.
2. Initialize the first element of the arrayL and last element of arrayR.
3. If the current array element is greater than the previous element.
   1. Update the increasingNumber to the index.
   2. Assign the value increasingNumber to the arrayL.
4. Traverse the array from the right to the left and check if the number greater than the previous element (the element to the right of the current element).
   1. Then update the decreasingNumber to the index
   2. Assign the arrayR to decreasingNumber.
5. For every given query, arrayR[left] is greater than the arrayL[right] return true, else return false.

Explanation

We have given an integer array and a range left, right. We have asked to find out if the subarray so formed with the given range can be a mountain array or not. If the subarray so formed is mountain array then we will return true, else return false. We will be declaring two arrays. One is for the left side of the array and the other is for the right side of the array. Then we will be building these arrays so that each query can give a solution in constant space.

We will initialize the first and the last element of the array we created arrayL and arrayR respectively. Then we traverse the array for the left side of the array or we can say from left to right. We will check the condition if the current array element is less than the previous element. If it is found to be true, then we will update the increasingNumber to the index of the number. And assign arrayL’s’ current element to the increasingNumber every time irrespectively of the condition is true or not.

In the next step we will be traversing the array from the right to left, basically from the second last element to the first element of the array, and checking if array’s current element is greater than the next element. Since we are traversing from right to left, we can say check with the previous element. If the condition is correct or true, then the decreasingNumber value is changed to the current index. Update the array to the decreasingNumber irrespective of the conditions. Return true, if the arrayR[left] is greater than or equal to the arrayL[right], else return false.

Code

C++ code to find whether a subarray is in form of a mountain or not

#include<iostream>

using namespace std;

void buildArrays(int arr[], int N, int arrayL[], int arrayR[])
{
    arrayL[0] = 0;
    int increasingNumber = 0;

    for (int i = 1; i < N; i++)
    {
        if (arr[i] > arr[i - 1])
            increasingNumber = i;
        arrayL[i] = increasingNumber;
    }
    arrayR[N - 1] = N - 1;
    int decreasingNumber = N - 1;

    for (int i = N - 2; i >= 0; i--)
    {
        if (arr[i] > arr[i + 1])
            decreasingNumber = i;
        arrayR[i] = decreasingNumber;
    }
}

bool solveQuery(int arr[], int arrayL[], int arrayR[], int Left, int Right)
{
    return (arrayR[Left] >= arrayL[Right]);
}

int main()
{
    int arr[] = {3,4,5,6,1,5,1,2,1};
    int N = sizeof(arr) / sizeof(int);

    int arrayL[N], arrayR[N];
    buildArrays(arr, N, arrayL, arrayR);

    int L = 0;
    int R = 3;
    if (solveQuery(arr, arrayL, arrayR, L, R))
        cout << "Mountain form\n";
    else
        cout << "Not a mountain form\n";

    L = 5;
    R = 7;
    if (solveQuery(arr, arrayL, arrayR, L, R))
        cout << "Mountain form\n";
    else
        cout << "Not a mountain form\n";

    return 0;
}

Mountain form
Not a mountain form

Java code to find whether a subarray is in form of a mountain or not

class MountainArray
{
    static void buildArrays(int arr[], int N, int arrayL[], int arrayR[])
    {
        arrayL[0] = 0;
        int increasingNumber = 0;

        for (int i = 1; i < N; i++)
        {
            if (arr[i] > arr[i - 1])
                increasingNumber = i;
            arrayL[i] = increasingNumber;
        }
        arrayR[N - 1] = N - 1;
        int decreasingNumber = N - 1;

        for (int i = N - 2; i >= 0; i--)
        {
            if (arr[i] > arr[i + 1])
                decreasingNumber = i;
            arrayR[i] = decreasingNumber;
        }
    }
    
    static boolean solveQuery(int arr[], int arrayL[], int arrayR[], int Left, int Right)
    {
        return (arrayR[Left] >= arrayL[Right]);
    }

    public static void main(String[] args)
    {
        int arr[] = {3,4,5,6,1,5,1,2,1};
        int N = arr.length;
        int arrayL[] = new int[N];
        int arrayR[] = new int[N];
        buildArrays(arr, N, arrayL, arrayR);
        int L = 0;
        int R = 3;

        if (solveQuery(arr, arrayL, arrayR, L, R))
            System.out.println("Mountain form");
        else
            System.out.println("Not a mountain form");

        L = 5;
        R = 7;

        if (solveQuery(arr, arrayL, arrayR, L, R))
            System.out.println("Mountain form");
        else
            System.out.println("Not a mountain form");
    }
}

Mountain form
Not a mountain form

Complexity Analysis

Time Complexity

O(N+Q), we require O(N) time for building both the arrays. And once the arrays are built. We can answer the queries in O(1).

Space Complexity

O(n) where “n” is the number of elements in the array.