Table of Contents
Problem Statement
The “Gold Mine problem” states that you are given a 2D grid having some non-negative coins placed in each cell of the given grid. Initially, the miner is standing at the first column but there is no restriction on the row. He can start in any row. The miner can move only in the right direction to the just next column. He can also move in diagonals. So from each cell, you have three directions, just to the right, top right, or bottom right. But the cell should be inside the boundary of the grid. You need to find what is the maximum amount of gold coins that he can collect?
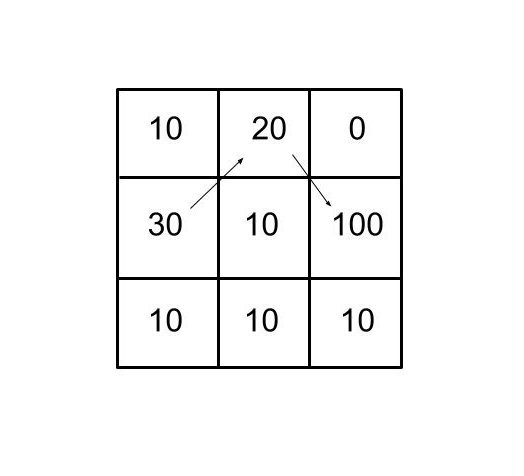
matrix = {{10, 20, 0},
{30, 10, 100},
{10, 10, 10}}The maximum coins he can collect = 150
Explanation: See the image for the path, miner should choose for collecting 150 gold coins.
Approach for Gold Mine Problem
A naive approach can be to use backtracking to produce all the paths that a miner can take from the first column to the last column. And for each path calculate the number of gold coins collected on each path. But this approach is time-consuming and will exceed the time limit as we increase the size of the grid.
A better approach will be to use some facts which are known to us. We know that miner can come to the current cell only from three cells, the cell which is just to the left of current cell, the cell which is just above this left cell, and the cell which just to the bottom of this left cell. So we can take the maximum of these three values will give us the maximum coins which can be collected if we are at the current cell. So, we will use dynamic programming to store the result for any current cell. That is the maximum number of coins that can be collected if the miner comes to the current cell.
Code
C++ code for Gold Mine problem
#include<bits/stdc++.h>
using namespace std;
int main()
{
// grid size n*m
int n,m;cin>>n>>m;
int a[n][m]; // grid storing the number of gold coins in each cell
// taking input of the grid storing the number of gold coins
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
cin>>a[i][j];
}
/*
^ ^ ^
\
^- & ^
/
^ ^ ^
Consider this represents a grid and we are currently at a cell having & stored in it.
So only there are three cells from which miner could have reached current cell
So we take maximum of all the options and thus at the end in the last corner
We receive the largest amount of gold coins.
*/
for(int j=1;j<m;j++){
for(int i=0;i<n;i++)
a[i][j] += max({((i>0) ? a[i-1][j-1] : 0), a[i][j-1], ((i+1<n) ? a[i+1][j-1] : 0)});
}
int ans = 0;
for(int i=0;i<n;i++){
ans = max(ans, a[i][m-1]);
}
cout<<ans<<endl;
}3 3 10 20 0 30 10 100 10 10 10
150
Java code for Gold Mine problem
import java.util.*;
class Main{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();// grid size n*m
int m = sc.nextInt();
int a[][] = new int[n][m]; // grid storing the number of gold coins in each cell
// taking input of the grid storing the number of gold coins
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
a[i][j] = sc.nextInt();
}
/*
^ ^ ^
\
^- & ^
/
^ ^ ^
Consider this represents a grid and we are currently at a cell having & stored in it.
So only there are three cells from which miner could have reached current cell
So we take maximum of all the options and thus at the end in the last corner
We receive the largest amount of gold coins.
*/
for(int j=1;j<m;j++){
for(int i=0;i<n;i++){
int topLeft = ((i>0) ? a[i-1][j-1] : 0);
int justLeft = a[i][j-1];
int bottomLeft = ((i+1<n) ? a[i+1][j-1] : 0);
int maxOfAll = Math.max(topLeft, bottomLeft);
maxOfAll = Math.max(maxOfAll, justLeft);
a[i][j] += maxOfAll;
}
}
int ans = 0;
for(int i=0;i<n;i++){
ans = Math.max(ans, a[i][m-1]);
}
System.out.println(ans);
}
}3 3 10 20 0 30 10 100 10 10 10
150
Complexity Analysis
Time Complexity
O(N*M), cause we had to traverse through all of the grid. And since it has N*M cells. The time complexity is polynomial.
Space Complexity
O(1), since we have used the initial matrix to work upon. We did not use any extra matrix/grid to store the intermediate results. But the program as a whole requires O(N*M) space complexity.