Longest Common Subsequence

Difficulty Level Medium
Frequently asked in Amazon eBay Facebook Morgan Stanley
Dynamic Programming StringViews 4287

You are given two strings str1 and str2, find out the length of the longest common subsequence.

Subsequence: a subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements. For ex ‘tticp‘ is the subsequence of ‘tutorialcup‘.

Example

input : str1 = "AGCA", str2 = "GAC"
sol   : longest common subsequence (LCA) = "GA"
        length of LCA = 2  
output: 2
   
input : str1 = "ABC", str2 = "XYZ"
sol   : No common character found
        length of LCA = 0
output: 0
    
input : str1 = "MZJAWXU", str2 = "XMJYAUZ"
sol   : longest common subsequence (LCA) = "MJAU"
        length of LCA = 4
output: 4

Types of Solution

  1. Naive
  2. Recursive
  3. using Dynamic Programming
    • Memoized solution.
    • Tabulated solution.
    • Space Optimized tabulated solution

we will discuss each of the solutions below.

Naive

let’s assume we have two strings of length m and n.

The idea of the Naive solution is to generate all the subsequences of both str1 and str2, compare each of the subsequences one by one. The largest matching subsequence would be our required answer.

There are total of 2m-1 and 2n-1 subsequence of strings str1 (length = m) and str1(length = n). Therefore, Time complexity to generate all the subsequences is O(2n+2m) ~ O(2n).  Additionally, it would take O(mn) time to compare each of the subsequences and output the common and longest one. Therefore, overall time complexity becomes O(mn*2n). This time complexity is computationally very intensive and can be improved further.

Recursive Solution for Longest Common Subsequence

Algorithm

consider two strings str1 and str2 of lengths n and m. LCS(m,n) is length of longest common subsequence of str1 and str2.

  1. start comparing strings from their right end.
  2. if m or n is 0, return 0.
  3. if str1[m-1] == str2[n-1] (if end characters match) , return 1+LCS(m-1,n-1). Recursively call LCS(m-1,n-1) and add 1 to it.
  4. else if str1[m-1] != str2[n-1] (if end characters don’t match), return max(LCS(m-1,n),LCS(m,n-1)). i.e. Recursively call LCS(m-1,n) and LCS(m,n-1) and return it’s maximum.

C++ Program

#include <iostream>
using namespace std;

int LCS(string str1,string str2,int m,int n)
{
    // if length of any string is 0, return 0
    if(n == 0 || m == 0)
    return 0;
    
    // if last characters match, remove them
    // then find LCS of remaining strings
    if(str1[m-1] == str2[n-1])
    return 1+LCS(str1,str2,m-1,n-1);
    
    // if last characters dont match
    // alternately remove last character of each string
    // to find LCS
    return max(LCS(str1,str2,m,n-1),LCS(str1,str2,m-1,n));
}

int main() 
{
  string str1 = "AGCA";
  string str2 = "GAC";
  
  int m = str1.length();
  int n = str2.length();
  
  cout<<"length of LCS : "<<LCS(str1,str2,m,n)<<endl;
  
  return 0;
}
Length of LCS : 2

Java Program

class tutorialcup
{
    static int LCS(String str1,String str2,int m,int n)
    {
        // if length of any string is 0, return 0
        if(n == 0 || m == 0)
        return 0;
        
        // if last characters match, remove them
        // then find LCS of remaining strings
        if(str1.charAt(m-1) == str2.charAt(n-1))
        return 1+LCS(str1,str2,m-1,n-1);
        
        // if last characters dont match
        // alternately remove last character of each string
        // to find LCS
        return Math.max(LCS(str1,str2,m-1,n),LCS(str1,str2,m,n-1));
    }
    
    public static void main(String args[])
    {
        String str1 = "AGCA";
        String str2 = "GAC";
        
        int m = str1.length();
        int n = str2.length();
        
        System.out.print("Length of LCS : "+LCS(str1,str2,m,n));
    }
}
Length of LCS : 2

Complexity Analysis

  1. Time complexity : T(n) = O(2n) , exponential time complexity.
  2. Space Complexity : A(n) = O(1)

n = length of larger string.

Dynamic Programming

The idea of dynamic programming is to simply store/save the results of various subproblems calculated during repeated recursive calls so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial. Consider the following recursion tree diagram of LCS(“AGCA”, “GAC”) :

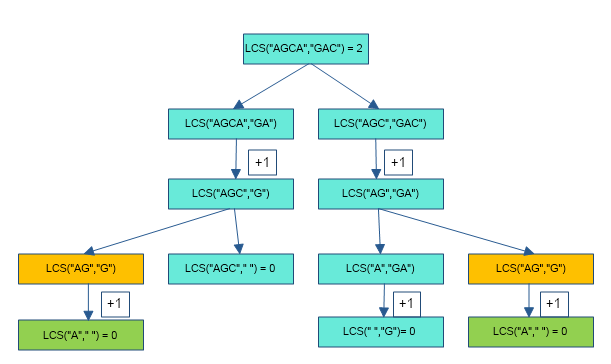
Longest Common Subsequence

We observe that solutions for subproblems LCS(“AG”,”G”) and LCS(“A”,” “) are evaluated (as 1 & 0 respectively) repeatedly. this repeated calculation of solution of the same subproblems occurs more often in case of larger strings. The extra effort in calculating the same subproblem repeatedly costs time overhead and increases the complexity of the algorithm.

The objective of Dynamic Programming Solution is to store/save solutions of subproblems and produce them (instead of calculating again) whenever the algorithm requires that particular solution. This method hugely reduces the time complexity.

It is observed that time complexity is reduced from exponential order to polynomial order which is less computationally intensive.

Memoized Solution  for Longest Common Subsequence

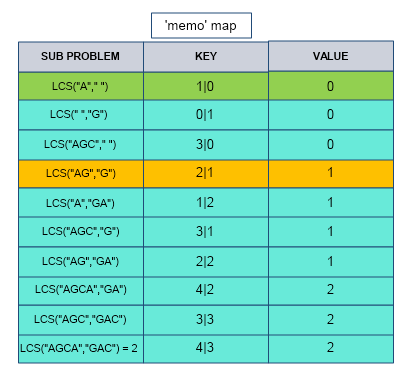
We save/store the solution of each subproblem. This is done using a Map data structure where the subproblem is the key and its numerical solution is the value. In simpler words, we map the subproblem (key) to the solution (value). The subproblem is converted to a string and mapped to a numerical solution. we create a Map ‘memo’, this memo has subproblems (string data type) as key and solution(Integer data type) as value.

When we call LCS for a subproblem, we check whether the solution to that subproblem has been stored in the Map or not.If it is already stored, we directly use that value or else calculate the value.

The following table shows subproblems, their corresponding keys, and values :

Longest Common Subsequence

C++ Program

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

int LCS(string str1,string str2,int m,int n,unordered_map<string,int>& memo)
{
    // return if we have reached the end of either string
  if (n == 0 || m == 0)
    return 0;

  // construct an unique map key from dynamic elements of the input
  string key = to_string(m) + "|" + to_string(n);

  // if sub-problem is seen for the first time, solve it and
  // store its result in a map
  if (memo.find(key) == memo.end())
  {
    // if last character of str1 and str2 matches
    if (str1[m - 1] == str2[n - 1])
      memo[key] = 1 + LCS(str1, str2, m - 1, n - 1, memo);

    else
    // else if last character of str1 and str2 don't match
    memo[key] = max(LCS(str1, str2, m, n - 1, memo),
            LCS(str1, str2, m - 1, n, memo));
  }

  // return the subproblem solution from the map
  return memo[key];
}

int main() 
{
  string str1 = "AGCA";
  string str2 = "GAC";
  
  // we use map to store memoized values
  unordered_map <string,int> memo;
  
  int m = str1.length();
  int n = str2.length();
  
  cout<<"length of LCS : "<<LCS(str1,str2,m,n,memo)<<endl;
  
  return 0;
}
Length of LCS : 2

Java Program

import java.util.HashMap;
class tutorialcup
{
    static int LCS(String str1,String str2,int m,int n,HashMap <String,Integer> memo)
    {
        // return if we have reached the end of either string
    	if (n == 0 || m == 0)
    		return 0;
    
    	// construct an unique map key from dynamic elements of the input
    	String key = m + "|" + n;
    
    	// if sub-problem is seen for the first time, solve it and
    	// store its result in a map
    	if (!memo.containsKey(key))
    	{
    		// if last character of str1 and str2 matches
    		if (str1.charAt(m-1) == str2.charAt(n-1))
    			memo.put(key,1 + LCS(str1, str2, m - 1, n - 1, memo));
    
    		else
    		// else if last character of str1 and str2 don't match
    		memo.put(key,Math.max(LCS(str1, str2, m, n - 1, memo),
    						LCS(str1, str2, m - 1, n, memo)));
    	}
    
    	// return the subproblem solution from the map
    	return memo.get(key);
    }

    
    public static void main(String args[])
    {
        String str1 = "AGCA";
        String str2 = "GAC";
        // we use map to store memoized values
        HashMap <String,Integer> memo = new HashMap <String,Integer>();
        
        int m = str1.length();
        int n = str2.length();
        
        System.out.print("Length of LCS : "+LCS(str1,str2,m,n,memo));
    }
}
Length of LCS : 2

Complexity Analysis

  1. Time complexity : T(n) = O(mn) , polynomial time complexity.
  2. Space Complexity : A(n) = O(mn), polynomial space complexity.

m = length of str1, n = length of str2

Tabulated Solution for Longest Common Subsequence

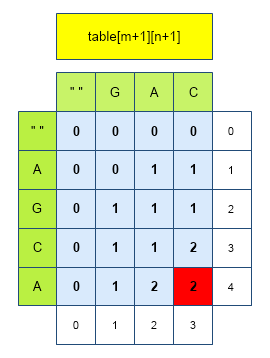
The objective of this solution is to again store the numerical solution of each of the subproblems, but using a different data structure. In this case, we utilize a table (2D array or matrix) to store solutions to the subproblems. The indices of the table are subproblems and value at that indices is the numerical solution for that particular subproblem.

Table obtained for LCS(“AGCA”,”GAC”) is

Longest Common Subsequence

C++ Program

#include<bits/stdc++.h> 
using namespace std; 

/* Returns length of LCS for str1 and str2 */
int LCS(string str1, string str2) 
{ 
    int m = str1.length();
    int n = str2.length();
    
    // matrix to store value of each subproblem
    int table[m+1][n+1]; 
    int i, j; 
  
  // Following steps build table[m+1][n+1] in bottom up fashion. 
  // value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
  for (i = 0; i <= m; i++) 
  { 
    for (j = 0; j <= n; j++) 
    { 
    		if (i == 0 || j == 0) 
    		    table[i][j] = 0;
    	
    		else if (str1[i-1] == str2[j-1]) 
    			table[i][j] = 1 + table[i-1][j-1]; 
    	
    		else
    			table[i][j] = max(table[i-1][j], table[i][j-1]); 
    } 
  } 
    
  // table[m][n] contains length of LCS for str1[0,n-1] and str2[0,m-1] 
  return table[m][n]; 
} 

// main function to implement above functions
int main() 
{ 
  string str1 = "AGCA"; 
  string str2 = "GAC"; 
  
  cout << "Length of LCS : "<< LCS(str1,str2); 
  
  return 0; 
} 



Length of LCS : 2

Java Program

class tutorialcup
{
    static int LCS(String str1, String str2)
    {
        int m = str1.length();
        int n = str2.length();
        
        // matrix to store value of each subproblem
        int[][] table = new int[m+1][n+1]; 
    	int i, j; 
    	
    	// Following steps build table[m+1][n+1] in bottom up fashion. 
    	// value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
    	for (i = 0; i <= m; i++) 
    	{ 
    		for (j = 0; j <= n; j++) 
    		{ 
        		if (i == 0 || j == 0) 
        		    table[i][j] = 0;
        	
        		else if (str1.charAt(i-1) == str2.charAt(j-1)) 
        			table[i][j] = 1 + table[i-1][j-1]; 
        	
        		else
        			table[i][j] = Math.max(table[i-1][j], table[i][j-1]); 
    		} 
    	} 
    	
    	for(i=0;i<=m;i++)
    	{
    	    for(j=0;j<=n;j++)
    	    System.out.print(table[i][j]+" ");
    	    
    	    System.out.println();
    	}
    		
    	// table[m][n] contains length of LCS for str1[0,n-1] and str2[0,m-1] 
    	return table[m][n]; 
    }
    
    // main function to implement above functions
    public static void main(String args[])
    {
        String str1 = "AGCA";
        String str2 = "GAC";
        
        System.out.println("Length of LCS : "+LCS(str1,str2));
        
        
    }
}
Length of LCS : 2

Complexity Analysis

  1. Time complexity : T(n) = O(mn) , polynomial time complexity.
  2. Space Complexity : A(n) = O(mn), for DP table

m = length of str1, n = length of str2

Space Optimized Tabulated Solution for Longest Common Subsequence

we observe in the above tabulation solution that in each iteration of the outer loop we need only values from immediate previous rows. So we don’t need to store all the rows in our ‘table’ matrix, we can just store two rows at a time and use them, in that way used space will reduce from table[m+1][n+1] to table[2][n+1].

Below we implement the algorithm.

C++ Program

#include<bits/stdc++.h> 
using namespace std; 

/* Returns length of LCS for str1 and str2 */
int LCS(string str1, string str2) 
{ 
    int m = str1.length();
    int n = str2.length();
    
    // matrix to store value of each subproblem
    int table[2][n+1]; 
    int i, j; 
    
    // binary index used to access current and previous rows
    bool index;
  
  // Following steps build table[m+1][n+1] in bottom up fashion. 
  // value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
  for (i = 0; i <= m; i++) 
  { 
      // calculate the current binary index
      index = i & 1;
      
    for (j = 0; j <= n; j++) 
    { 
    		if (i == 0 || j == 0) 
    		    table[index][j] = 0;
    	
    		else if (str1[i-1] == str2[j-1]) 
    			table[index][j] = 1 + table[1-index][j-1]; 
    	
    		else
    			table[index][j] = max(table[1-index][j], table[index][j-1]); 
    } 
  } 
    
  // Last filled entry contains 
    // length of LCS for str1[0,n-1] and str2[0,m-1]  
  return table[index][n]; 
} 

// main function to implement above functions
int main() 
{ 
  string str1 = "AGCA"; 
  string str2 = "GAC"; 
  
  cout << "Length of LCS : "<< LCS(str1,str2); 
  
  return 0; 
} 

Length of LCS : 2

Java Program

class tutorialcup
{
    static int LCS(String str1, String str2)
    {
        int m = str1.length();
        int n = str2.length();
        
        // matrix to store value of each subproblem
        int[][] table = new int[2][n+1]; 
        int i, j; 
        
        // binary index used to access current and previous rows
        int index = 1;
    	
    	// Following steps build table[m+1][n+1] in bottom up fashion. 
    	// value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
    	for (i = 0; i <= m; i++) 
    	{ 
    	    // calculate the current binary index
    	    index = i & 1;
    	    
    		for (j = 0; j <= n; j++) 
    		{ 
        		if (i == 0 || j == 0) 
        		    table[index][j] = 0;
        	
        		else if (str1.charAt(i-1) == str2.charAt(j-1)) 
        			table[index][j] = 1 + table[1-index][j-1]; 
        	
        		else
        			table[index][j] = Math.max(table[1-index][j], table[index][j-1]); 
    		} 
    	} 
    		
    	// Last filled entry contains 
        // length of LCS for str1[0,n-1] and str2[0,m-1]  
    	return table[index][n]; 
    }
    
    // main function to implement above functions
    public static void main(String args[])
    {
        String str1 = "AGCA";
        String str2 = "GAC";
        
        System.out.println("Length of LCS : "+LCS(str1,str2));
        
    }
}
Length of LCS : 2

Complexity Analysis

  1. Time complexity : T(n) = O(mn) , polynomial time complexity.
  2. Space Complexity : A(n) = O(n) , Linear space complexity

m = length of str1, n = length of str2

Printing the longest common subsequence

Algorithm

  1. construct a DP table the same as that mentioned in the tabulated solution.
  2. create an empty string, ‘lcs’.
  3. Traverse the table from rightmost bottomost cell, table[m][n].
  4. For every cell table[i][j] while traversing,do following :
    • If characters (in str1 and str2) corresponding to table[i][j] are same (i.e. str1[i-1] == str2[j-1]), then append this character to lcs.
    • Else compare values of table[i-1][j] and table[i][j-1] and move in direction (to cell) which has greater value.
  5. Since, characters are added from the right end, reverse the ‘lcs’ string to obtain the required longest common subsequence of str1 and str2.

C++ Program

#include <iostream>
#include <bits/stdc++.h> 
using namespace std; 

/* Returns length of LCS for str1 and str2 */
string LCS(string str1, string str2) 
{ 
    int m = str1.length();
    int n = str2.length();
    string lcs = "";
    
    // matrix to store value of each subproblem
    int table[m+1][n+1]; 
    int i, j; 
    
    
  // Following steps build table[m+1][n+1] in bottom up fashion. 
  // value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
  for (i = 0; i <= m; i++) 
  { 
    for (j = 0; j <= n; j++) 
    { 
    		if (i == 0 || j == 0) 
    		    table[i][j] = 0;
    	
    		else if (str1[i-1] == str2[j-1]) 
    			table[i][j] = 1 + table[i-1][j-1]; 
    	
    		else
    			table[i][j] = max(table[i-1][j], table[i][j-1]); 
    } 
  } 
    
  // Start from the right-most,bottom-most corner and one by one store characters in lcs 
  i = m,j = n;
  while(i > 0 && j > 0)
  {
      // if current characters match, then are part of LCS
      if(str1[i-1] == str2[j-1])
      {
          lcs.push_back(str1[i-1]);
          i--;
          j--;
      }
      
      // if current characters are not same 
      // then find larger of two cells(above and left)
      // and move in the direction of larger cell
      else if(table[i-1][j] > table[i][j-1])
      i--;
      else
      j--;
  }
  
  // since characters from string are appended from right end
  // we need to reverse the lcs string to obtain the actual string
  reverse(lcs.begin(),lcs.end());
  return lcs;
} 

// main function to implement above functions
int main() 
{ 
  string str1 = "AGCA"; 
  string str2 = "GAC"; 
  
  cout << "LCS of str1 and str2 : "<< LCS(str1,str2); 
  
  return 0; 
} 

LCS of str1 and str2 : GA

Java Program

class tutorialcup
{
    static StringBuilder LCS(String str1, String str2)
    {
        int m = str1.length();
        int n = str2.length();
        // use mutable string to store lcs
        StringBuilder lcs = new StringBuilder();
        
        // matrix to store value of each subproblem
        int[][] table = new int[m+1][n+1]; 
        int i, j; 
    
    	
    	// Following steps build table[m+1][n+1] in bottom up fashion. 
    	// value at table[i][j] contains length of LCS of str1[0,i-1] and str2[0,j-1]
    	for (i = 0; i <= m; i++) 
    	{ 
    		for (j = 0; j <= n; j++) 
    		{ 
        		if (i == 0 || j == 0) 
        		    table[i][j] = 0;
        	
        		else if (str1.charAt(i-1) == str2.charAt(j-1)) 
        			table[i][j] = 1 + table[i-1][j-1]; 
        	
        		else
        			table[i][j] = Math.max(table[i-1][j], table[i][j-1]); 
    		} 
    	} 
    	
    	// Start from the right-most,bottom-most corner and one by one store characters in lcs 
    	i = m;
    	j = n;
    	while(i > 0 && j > 0)
    	{
    	    // if current characters match, then are part of LCS
    	    if(str1.charAt(i-1) == str2.charAt(j-1))
    	    {
    	        lcs.append(str1.charAt(i-1));
    	        i--;
    	        j--;
    	    }
    	    
    	    // if current characters are not same 
    	    // then find larger of two cells(above and left)
    	    // and move in the direction of larger cell
    	    else if(table[i-1][j] > table[i][j-1])
    	    i--;
    	    else
    	    j--;
    	}
    	
    	// since characters from string are appended from right end
    	// we need to reverse the lcs string to obtain the actual string
    	lcs.reverse();
    	return lcs;
    	
    }
    
    // main function to implement above functions
    public static void main(String args[])
    {
        String str1 = "AGCA";
        String str2 = "GAC";
        
        System.out.println("LCS of str1 and str2 : "+LCS(str1,str2));
        
    }
}
LCS of str1 and str2 : GA

Application of LCS

  1. The longest common subsequence problem is a classic computer science problem, it is the basis of data comparison programs such as the diff utility.
  2. It has applications in computational linguistics and bioinformatics.
  3. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.

References

Translate »