In the longest palindromic subsequence problem we have given a string, find the length of the longest palindromic subsequence.
Table of Contents
Examples
Input:
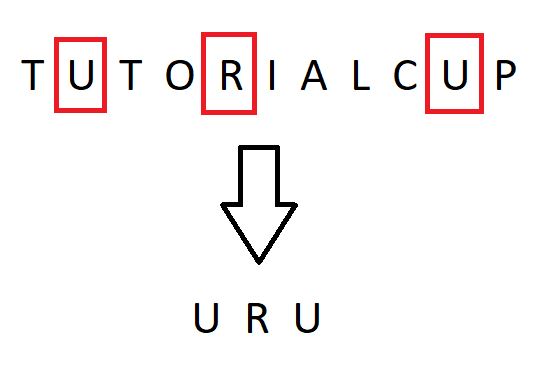
TUTORIALCUP
Output:
3
Input:
DYNAMICPROGRAMMING
Output:
7
Naive Approach for Longest Palindromic Subsequence
The naive approach to solve the above problem is to generate all the subsequences of the given string and find the length of the longest palindromic subsequence.
Time Complexity is exponential, which is very high.
Optimal Approach for Longest Palindromic Subsequence
The above problem posses an optimal substructure and overlapping property, so dynamic programming can be used to solve the problem.
Let the length of given string(s) be n, and longest palindromic subsequence length for s be represented as LPS(s, 0, n – 1).
s –> Given String
0 –> Starting index
n – 1 –> Ending index
- If the first and last characters of s(given string) are same, then,
LPS(s, 0, n – 1) = 2 + LPS(s, 1, n – 2 ) - Else,
LPS(s, 0, n – 1) = max (LPS(s, 0, n – 2), LPS(s, 1, n – 1)) - Base Case : Strings of length 1 are always palindrome, that is, LPS(s, i, i) = 1
- Base Case : If there are two characters in a string and both are same, then it is a palindrome.
Using this recursion and memoization, we can find the LPS in better time complexity.
Algorithm
- Create a 2-D array lps of size (n X n), where n is the length of string s, it stores the length of longest palindromic subsequence starting from x to y, where x is the row number and y is the column number and the answer to above problem is LPS[0][n – 1].
- We are given string s, the starting index i, and ending index e.
- If i and e are equal, return 1 (Base Case).
- If i + 1 = e and characters at i and e in s are same, return 2 (Base Case).
- Else if characters at position i and e in string s are equals return 2 + LPS(s, i + 1, e – 1).
- Else return max (LPS(s, i + 1, e), LPS(s, i, e – 1)).
- Before making any recursive call, check the corresponding value in lps array, that is, LPS(s, i, e) is present at lps[i][e], if there is no value in the lps array make a recursive call else use the calculated value. This step is responsible for reducing the time complexity of the algorithm.
Time Complexity = O(n^2)
JAVA Code for Longest Palindromic Subsequence
public class LongestPalindromicSubsequence {
// Function to return the length of longest palindromic subsequence
private static int LPS(String s) {
int n = s.length();
int[][] lps = new int[n][n];
return lpsUtil(s.toCharArray(), 0, n - 1, lps);
}
// Recursive utility function to calculate the length of longest palindromic subsequence
private static int lpsUtil(char[] s, int i, int e, int[][] lps) {
// Return if already calculated
if (lps[i][e] != 0) {
return lps[i][e];
}
// Base case (String of length 1 is always a palindrome)
if (i == e) {
lps[i][e] = 1;
return 1;
}
// Base Case (If there are only 2 characters and both are same)
if (s[i] == s[e] && i + 1 == e) {
lps[i][e] = 2;
return 2;
}
// If first and last characters are same then
// LPS(s, i, e) = 2 + LPS(s, i + 1, e - 1)
if (s[i] == s[e]) {
// If not calculated before, find the result and store in lps array
if (lps[i + 1][e - 1] == 0) {
lps[i + 1][e - 1] = lpsUtil(s, i + 1, e - 1, lps);
}
// Store the result in lps array
lps[i][e] = 2 + lps[i + 1][e - 1];
return lps[i][e];
} else {
// If not calculated before, find the result and store in lps array
if (lps[i + 1][e] == 0) {
lps[i + 1][e] = lpsUtil(s, i + 1, e, lps);
}
// If not calculated before, find the result and store in lps array
if (lps[i][e - 1] == 0) {
lps[i][e - 1] = lpsUtil(s, i, e - 1, lps);
}
// Store the result in lps array
lps[i][e] = Math.max(lps[i + 1][e], lps[i][e - 1]);
return lps[i][e];
}
}
public static void main(String[] args) {
// Example 1
System.out.println(LPS("TUTORIALCUP"));
// Example 2
System.out.println(LPS("DYNAMICPROGRAMMING"));
}
}C++ Code for Longest Palindromic Subsequence
#include <bits/stdc++.h>
#define MAXN 1000
using namespace std;
// Global array to store the lps for a given string
int lps[MAXN][MAXN];
// Recursive utility function to calculate the length of longest palindromic subsequence
int lpsUtil(string s, int i, int e) {
// Return if already calculated
if (lps[i][e] != 0) {
return lps[i][e];
}
// Base case (String of length 1 is always a palindrome)
if (i == e) {
lps[i][e] = 1;
return 1;
}
// Base Case (If there are only 2 characters and both are same)
if (s[i] == s[e] && i + 1 == e) {
lps[i][e] = 2;
return 2;
}
// If first and last characters are same then
// LPS(s, i, e) = 2 + LPS(s, i + 1, e - 1)
if (s[i] == s[e]) {
// If not calculated before, find the result and store in lps array
if (lps[i + 1][e - 1] == 0) {
lps[i + 1][e - 1] = lpsUtil(s, i + 1, e - 1);
}
// Store the result in lps array
lps[i][e] = 2 + lps[i + 1][e - 1];
return lps[i][e];
} else {
// If not calculated before, find the result and store in lps array
if (lps[i + 1][e] == 0) {
lps[i + 1][e] = lpsUtil(s, i + 1, e);
}
// If not calculated before, find the result and store in lps array
if (lps[i][e - 1] == 0) {
lps[i][e - 1] = lpsUtil(s, i, e - 1);
}
// Store the result in lps array
lps[i][e] = std::max(lps[i + 1][e], lps[i][e - 1]);
return lps[i][e];
}
}
// Function to return the length of longest palindromic subsequence
int LPS(string s) {
int n = s.length();
// Initialise lps as 0
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
lps[i][j] = 0;
}
}
return lpsUtil(s, 0, n - 1);
}
int main() {
// Example 1
cout<<LPS("TUTORIALCUP")<<endl;
// Example 2
cout<<LPS("DYNAMICPROGRAMMING")<<endl;
return 0;
}3 7