Moser-de Bruijn Sequence

Difficulty Level Medium
Frequently asked in FreeCharge Snapdeal Times Internet
Dynamic Programming SequenceViews 2045

In this problem, you are given an integer input n. Now you need to print the first n elements of the Moser-de Bruijn Sequence.

Example

7
0, 1, 4, 5, 16, 17, 20

Explanation

The output sequence has the first seven elements of the Moser-de Bruijn Sequence. Thus the output is absolutely correct.

Approach

In number theory, the Moser–de Bruijn sequence is an integer sequence named after Leo Moser and Nicolaas Govert de Bruijn, consisting of the sums of distinct powers of 4. So that means it will contain all the numbers which can be represented using distinct powers of 4.

We can also define the numbers which make up the Moser-de Bruijn Sequence in a little bit different manner. If the number converted into base-4 number system contains only 0 or 1. Then we say that the number exists in Moser-de Bruijn Sequence. It does not mean that the base-4 number system contains only 0 and 1 as its digits. Base-4 representation contains 0, 1, 2, and 3. But if the number exists in our sequence. It needs to follow some prerequisites which are to contain only 0 or 1 in base-4 representation. So now we are familiar with what type of numbers form the sequence. But how do we generate such numbers?

One simple way is to make use of the recurrence formula which is used to generate the numbers of the sequence. But there’s a catch.

The recurrence relation

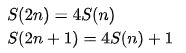
Moser-de Bruijn Sequence

The base case is for n = 0, S(0) = 0. Now, if we simply use the recurrence relation, we’ll be calculating some values more than once. This process will only add up to increase the time complexity. To improve our algorithm, we’ll store these values which will reduce the computations. This technique where we store the data which can be used later during computation is generally referred to as Dynamic Programming. Check out the basics of dynamic programming here.

Code

C++ code to generate Moser-de Bruijn Sequence

#include <bits/stdc++.h>
using namespace std;

int main(){
  // number of elements to be generated
  int n;cin>>n;
  if(n >= 1)cout<<0<<" ";
  if(n >= 2)cout<<1<<" ";
  if(n >= 3) {
    int dp[n];
    dp[0] = 0,dp[1] = 1;
    for(int i=2; i<n;i++){
      if(i%2 == 0)
        dp[i] = 4*dp[i/2];
      else
        dp[i] = 4*dp[i/2] + 1;
      cout<<dp[i]<<" ";
    }
  }
}
6
0 1 4 5 16 17

Java code to generate Moser-de Bruijn Sequence

import java.util.*;
class Main{
    public static void main(String[] args){
    	Scanner sc = new Scanner(System.in);
    // number of elements to be generated
    int n = sc.nextInt();
    if(n >= 1)System.out.print("0 ");
    if(n >= 2)System.out.print("1 ");
    if(n >= 3) {
      int dp[] = new int[n];
      dp[0] = 0;dp[1] = 1;
      for(int i=2; i<n;i++){
        if(i%2 == 0)
          dp[i] = 4*dp[i/2];
        else
          dp[i] = 4*dp[i/2] + 1;
        System.out.print(dp[i]+" ");
      }
    }
  }
}
6
0 1 4 5 16 17

Complexity Analysis

Time Complexity

O(N), because once a number is calculated, there is no time required to use it later in the computation. Since pre-computation requires O(N) time. The time, complexity is linear.

Space Complexity

O(N), because we have created a new DP array which is dependent on the input. The space complexity for the problem is linear.

Translate »