Table of Contents
Problem Statement
Given a string, find the minimum number of cuts required such that all the substrings of partitions are palindromes. Since we are cutting our original string into different partitions such that all the substrings are palindromes, we call this problem the Palindrome Partition Problem.
Example
asaaaassss
2
Explanation: Here, we can cut the input string as asa | aaa | ssss, thus we require two cuts.
zxxzxxzyuy
1
Explanation: Here, we can cut the input string as zxxzxxz | yuy, so we need a single cut.
Approach for Palindrome Partitioning
Naive Approach
The first thing that comes to mind is a simple recursive solution. Consider, we have a string of length say n. Now, if the string is palindrome we can simply return the answer 0 but if it isn’t a palindrome. We try all the possibilities, by that what I mean is we try cutting the string in two partitions at the kth index and then solve recursively for the left part and right part separately. This solution is absolutely correct but is not efficient though.
minCut(string s, int i, int j) = 1 + min( minCut(s, i, k) + minCut(s, k+1, j) ) where k ranges from i to j i, j, k are indices on string
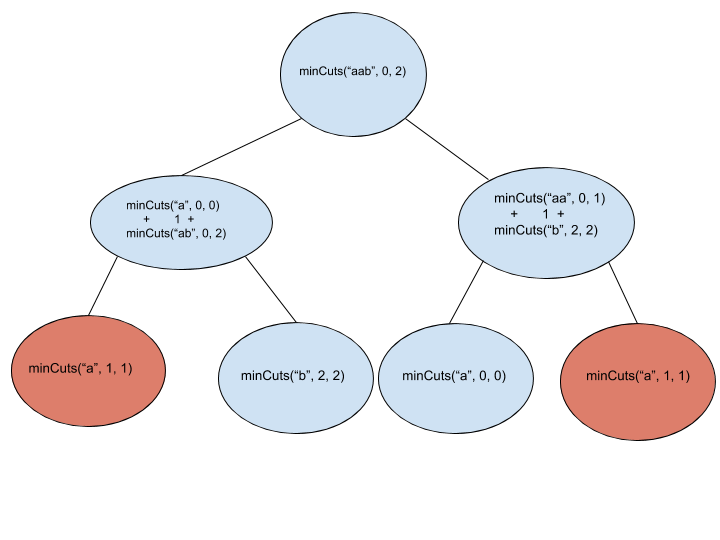
Efficient Approach
Until now, we know a simple solution that solves the left part and right part of the string while placing a cut between them. So, we can say that initially we had a problem with a string of size n and then we reduced our problem to two subproblems. If we see the structure of subproblems they surely overlap also. So, this suggests the use of Dynamic Programming to reduce the exponential time complexity of the earlier solution to O(N^3). The figure shows the overlapping subproblems in red. A similar Dynamic Programming pattern can be seen in Matrix Chain Multiplication Problem, where we first solve smaller subproblems and then combine their result for solving the original problem.
Code for Palindrome Partitioning
C++ Code
#include <bits/stdc++.h>
using namespace std;
int minCut(string s) {
int n = s.length();
vector<vector<int>> cuts;
vector<vector<bool>> isPalindrome;
cuts.assign(n,vector<int>(n, INT_MAX));
isPalindrome.assign(n, vector<bool>(n, false));
for(int len = 1;len<=n;len++) {
for(int i=0;i<n-len+1;i++) {
int j = i+len-1;
if(len <= 2)
isPalindrome[i][j] = s[i] == s[j];
else
isPalindrome[i][j] = s[i] == s[j] && isPalindrome[i+1][j-1];
if(isPalindrome[i][j]) {
cuts[i][j] = 0;
} else {
for(int k=i;k<j;k++)
cuts[i][j] = min(cuts[i][j], 1+cuts[i][k]+cuts[k+1][j]);
}
}
}
return cuts[0][n-1];
}
int main() {
int t;cin>>t;
while(t--){
string s;
cin>>s;
cout<<minCut(s)<<endl;
}
}
Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
public static int minCut(String s) {
int n = s.length();
int cuts[][] = new int[n][n];
boolean isPalindrome[][] = new boolean[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cuts[i][j] = Integer.MAX_VALUE;
}
}
for(int len = 1;len<=n;len++) {
for(int i=0;i<n-len+1;i++) {
int j = i+len-1;
if(len <= 2)
isPalindrome[i][j] = s.charAt(i) == s.charAt(j);
else
isPalindrome[i][j] = s.charAt(i) == s.charAt(j) && isPalindrome[i+1][j-1];
if(isPalindrome[i][j]) {
cuts[i][j] = 0;
} else {
for(int k=i;k<j;k++)
cuts[i][j] = Math.min(cuts[i][j], 1+cuts[i][k]+cuts[k+1][j]);
}
}
}
return cuts[0][n-1];
}
public static void main (String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
while(t-- > 0) {
String s = br.readLine();
int ans = minCut(s);
System.out.println(ans);
}
}
}
Time Complexity: O(N^3)
The first loop runs from 1 to n (len = 1 to len = n)
The nested loop stating the start index for subproblem ( i ) runs from 0 to n-len
The most inner loop, which states the index of cut between k and k+1, also runs from i to j.
Thus, in the worst case, the time complexity is said to be O(N^3).
Space Complexity: O(N^2)
We have two arrays isPalindrome and cuts which are 2D arrays and thus we have O(N^2) space complexity.
Optimized Solution for Palindrome Partitioning
We can further reduce the time complexity to O(N^2), by pre-computing the isPalindrome matrix. Then instead of storing cuts for substring from i to j (where i is the left boundary and j is the right boundary of any palindrome substring), we store the cuts as a single-dimensional array storing the minimum number of cuts required for substring starting from 0 to i. The inner loop runs on j from 0 to i-1, where we check if substring [j,i] is palindrome? If substring is palindrome then the substring [j,i] has the same number of cuts as that of substring [0,j-1] + 1. So, we just update the answer by storing the minimum of all the options for j from 0 to i-1. This way, in the end, we have the minimum number of cuts required such that all the partitions are palindromes.
C++ Code
#include <bits/stdc++.h>
using namespace std;
int minCut(string s) {
int n = s.length();
vector<int> cuts;
vector<vector<bool>> isPalindrome;
cuts.assign(n,INT_MAX);
isPalindrome.assign(n, vector<bool>(n, false));
for(int len = 1;len<=n;len++) {
for(int i=0;i<n-len+1;i++) {
int j = i+len-1;
if(len <= 2)
isPalindrome[i][j] = s[i] == s[j];
else
isPalindrome[i][j] = s[i] == s[j] && isPalindrome[i+1][j-1];
}
}
cuts[0] = 0;
for(int i=1;i<n;i++) {
for(int j=1;j<=i;j++)
if(isPalindrome[0][i])
cuts[i] = 0;
else if(isPalindrome[j][i])
cuts[i] = min(cuts[i], 1 + cuts[j-1]);
}
return cuts[n-1];
}
int main() {
int t;cin>>t;
while(t--){
string s;
cin>>s;
cout<<minCut(s)<<endl;
}
}Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
public static int minCut(String s) {
int n = s.length();
int cuts[] = new int[n];
boolean isPalindrome[][] = new boolean[n][n];
for(int i=0;i<n;i++) {
cuts[i] = Integer.MAX_VALUE;
}
for(int len = 1;len<=n;len++) {
for(int i=0;i<n-len+1;i++) {
int j = i+len-1;
if(len <= 2)
isPalindrome[i][j] = s.charAt(i) == s.charAt(j);
else
isPalindrome[i][j] = s.charAt(i) == s.charAt(j) && isPalindrome[i+1][j-1];
}
}
cuts[0] = 0;
for(int i=1;i<n;i++) {
for(int j=1;j<=i;j++)
if(isPalindrome[0][i])
cuts[i] = 0;
else if(isPalindrome[j][i])
cuts[i] = Math.min(cuts[i], 1 + cuts[j-1]);
}
return cuts[n-1];
}
public static void main (String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
while(t-- > 0) {
String s = br.readLine();
int ans = minCut(s);
System.out.println(ans);
}
}
}
Time Complexity: O(N^2)
We took O(N^2) for storing if the substring from index to j is palindrome.
The, O(N^2) for finding minimum number of cuts. Since the outer loop runs over the complete length of the string and the inner loop runs from 0 to i-1.
Thus, making runtime a total of O(N^2).
Space Complexity: O(N^2)
Even though our cuts array is now single-dimensional, our isPalindrome is still a 2D array.