Path with maximum average value

Difficulty Level Easy
Frequently asked in Cisco Epic Systems GreyOrange SAP Labs Times Internet
Array Dynamic Programming MatrixViews 2937

Problem Statement

The problem “Path with maximum average value” states that you are given a 2D array or a matrix of integers. Now consider you are standing at the top-left cell and need to reach the bottom right. For reaching the destination, you need to move along either in the bottom direction or in the right direction. by destination, here we mean the bottom-right cell. One condition is there, that you need to move along such a path which gives us a maximum average value.

Example

3 3 // number of rows and columns
1 1 2
10 1 100
10 10 1
22.6

Explanation

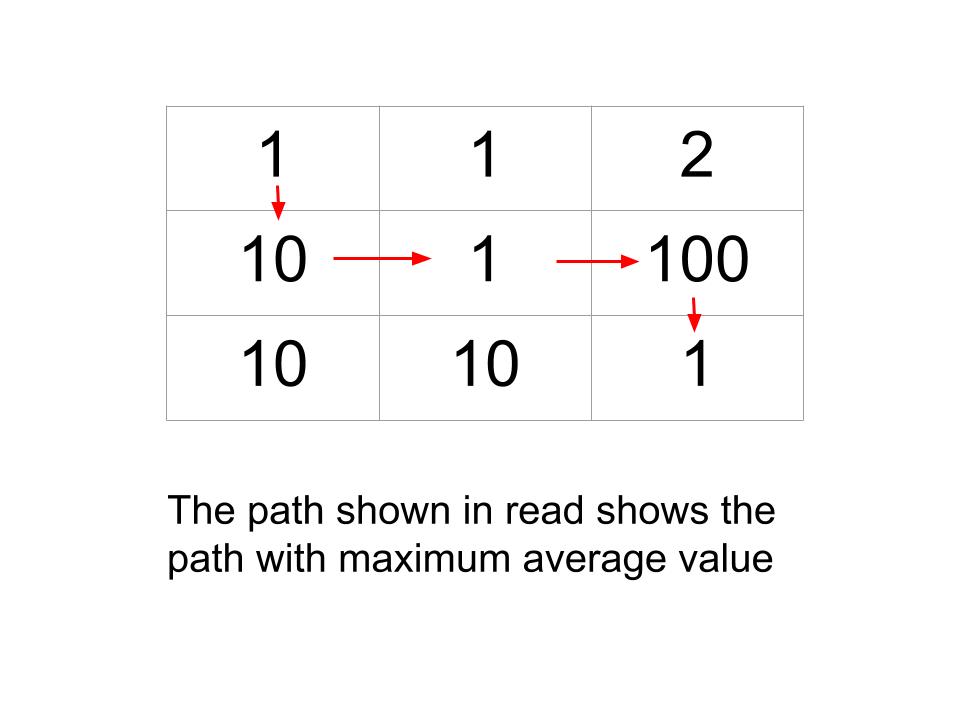
Path with maximum average value

We moved from the top-left cell in the following manner: 1-> 10-> 1-> 100-> 1. So adding this up gives us a total sum of 113. The average thus becomes equal to 113/5 = 22.6

Approach

One can come up with a brute force approach, which is to generate all the possible ways to reach the bottom-right cell. Once you have generated all the paths. Now move on them and find the sum of integers that lie on the path. So, once you have all the sums. Find the sum which is maximum among these.

But using this approach is sure to go into TLE or will exceed the time limit. Because the generation of such paths will lead to exponential time complexity. So, to solve the problem under time constraints. We need to find an efficient solution. But, how can we do that? We can do that using Dynamic Programming. And the problem also resembles very much to the Maximum Path Sum problem. In that problem, we need to find the maximum path sum in a 2D array. The same is what we are going to do, But in the end, we will take the average.

So for the Dynamic Programming approach. We will create a 2D DP array where each cell in DP matric will denote the maximum sum which can be attained if we need to start from the top left corner to the current cell. So we can write a general recurrence relation.

// Base Cases
dp[0][0] = a[0][0]
dp[i][0] = dp[i-1][0] + a[i][0] // here i starts from 1st row until the last row of matrix
dp[0][i] = dp[0][i-1] + a[0][i] // here i starts from 1st column until the last column of matrix
// Recurrence Relation
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + a[i][j] // for all other cells

C++ code for Path with maximum average value

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main(){
  int n,m; // number of rows and columns in input matrix
  cin>>n>>m;

  int input[n][m];
  for(int i=0;i<n;i++){
    for(int j=0;j<m;j++)
      cin>>input[i][j];
  }

  int dp[n][m];
  dp[0][0] = input[0][0];
  for(int i=1;i<n;i++)
    dp[i][0] = dp[i-1][0] + input[i][0];
  for(int i=1;i<m;i++)
    dp[0][i] = dp[0][i-1] + input[0][i];

  for(int i=1;i<n;i++){
    for(int j=1;j<m;j++)
      dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + input[i][j];
  }

  // division by n+m-1, because you need to travel at least n+m-1 cells to reach bottom right cell
  cout<<(dp[n-1][m-1]/((double)n+m-1));
}

3 3
1 1 2
10 1 100
10 10 1
22.6

Java code for Path with maximum average value

import java.util.*;

class Main{
  public static void main(String[] args){
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt(); int m = sc.nextInt(); // number of rows and columns in input matrix

    int input[][] = new int[n][m];
    for(int i=0;i<n;i++){
      for(int j=0;j<m;j++)
        input[i][j] = sc.nextInt();
    }

    int dp[][] = new int[n][m];
    dp[0][0] = input[0][0];
    for(int i=1;i<n;i++)
      dp[i][0] = dp[i-1][0] + input[i][0];
    for(int i=1;i<m;i++)
      dp[0][i] = dp[0][i-1] + input[0][i];

    for(int i=1;i<n;i++){
      for(int j=1;j<m;j++)
        dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]) + input[i][j];
    }

    // division by n+m-1, because you need to travel at least n+m-1 cells to reach bottom right cell
    System.out.print(dp[n-1][m-1]/((double)n+m-1));
  }
}
3 3
1 1 2
10 1 100
10 10 1
22.6

Complexity Analysis

Time Complexity

O(N^2) since we have simply traversed over the input array. And the transition in our DP took only O(1) time.

Space Complexity

O(N^2) since we created a 2D DP array.

Translate »