Print Fibonacci sequence using 2 variables

Problem Statement

The problem “Print Fibonacci sequence using 2 variables” states that you need to print the Fibonacci sequence but there is a limitation of using only 2 variables.

Example

n = 5

0 1 1 2 3 5

Explanation

The output sequence has the first five elements of the Fibonacci series.

Approach

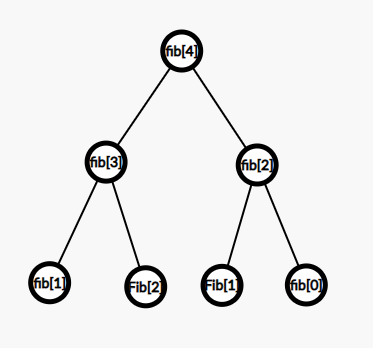
We are provided with a single element as input, which tells us the number of elements that need to be produced of the fibonacci sequence. So the naive approach to print Fibonacci sequence is recursion. Then we can use a loop that calls our recursive function for calculation of each fibonacci number. But this approach requires exponential time and thus we need something more efficient.

We can think of dynamic programming/memoization for the problem. The approach will surely reduce the time complexity. The exponential time complexity will be reduced to linear time complexity. But this approach still requires us linear space complexity. We need to reduce this space complexity further. What we can do is try to optimize the dynamic programming approach.

If we see the recursive formula, F(n) = F(n-1) + F(n-2). We are only dependent on the last two Fibonacci numbers. Thus we can only store the last two Fibonacci numbers to find the current number and this makes the algorithm run in O(1) space complexity.

Code

C++ code to Print Fibonacci sequence using 2 variables

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n;cin>>n;
    int last = 1, lastToLast = 0;
    if(n>=0)
        cout<<lastToLast<<" ";
    if(n>=1)
        cout<<last<<" ";
    for(int i=2;i<=n;i++){
        int cur = last + lastToLast;
        cout<<cur<<" ";
        lastToLast = last;
        last = cur;
    }
}

5

0 1 1 2 3 5

Java code to Print Fibonacci sequence using 2 variables

import java.util.*;
class Main{
  
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    	int last = 1, lastToLast = 0;
      if(n>=0)
          System.out.print(lastToLast+" ");
      if(n>=1)
          System.out.print(last+" ");
      for(int i=2;i<=n;i++){
          int cur = last + lastToLast;
          System.out.print(cur+" ");
          lastToLast = last;
          last = cur;
      }
  	}
}

5

0 1 1 2 3 5

Complexity Analysis

Time Complexity

O(N), because we have traversed only until the number of elements we require to print. First, we thought of solving the problem using recursion but that was exponential in time. Then we reduced our time complexity when we used dynamic programming. Because of which we were able to solve the problem in linear time.

Space Complexity

O(1),  we have solved the problem in constant space complexity because we have used only two variables.