Print Maximum Length Chain of Pairs

Difficulty Level Medium
Frequently asked in Amazon
Dynamic ProgrammingViews 1474

Problem Statement

The problem “Print Maximum Length Chain of Pairs” states that you are given some pairs of numbers. It is given that in each pair, the first number is smaller than the second number. Now you need to find the longest chain such that the second number of preceding pair (a, b) is smaller than the first number of next after pair(c, d) that is (b < c).

Example

(1, 10), (11, 25), (26, 35), (36, 50)
(1, 10), (11, 25), (26, 35), (36, 50)

Explanation

We selected all of the pairs because all of the given pairs satisfied the condition.

(1, 2), (10, 30), (5, 6), (15, 25), (17, 21)
(1, 2), (5, 6), (10, 30)

Explanation

The third pair which we selected does not matter. We could have selected any of the three remaining pairs because they all satisfied the condition. But we can not choose any two of the three remainings.

Approach to print Maximum Length Chain of Pairs

The problem asks us to find and print the maximum length chain of pairs. So what does the maximum length here means? The maximum length here represents the number of pairs in the result. So in the end, we need to find those pairs which constitute the maximum length.

We have already discussed this problem. The problem which we discussed asked us to find the maximum length. There we discussed different approaches to tackle the problem. Here in this part of the problem, we also need to find such pairs. We will solve the problem using Dynamic Programming because solving this using recursion will exceed the time limits. The recurrence relation is very similar to that of LIS (Longest Increasing Subsequence). We will create a vector of vectors. Each element of this vector of vectors will denote the pairs which make the maximum length sequence when we always choose the element corresponding to the current element in the input.

So, the recurrence relation is

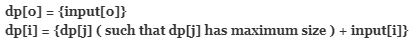
Print Maximum Length Chain of Pairs

Code

C++ code to Print Maximum Length Chain of Pairs

#include <bits/stdc++.h>
using namespace std;


void maxChainLength(vector<pair<int,int>> &input) 
{ 
    sort(input.begin(), input.end());
  
    int n = input.size();
    vector<vector<pair<int,int>>> dp(n); 
  	int mx = 0;
    // base case
    dp[0].push_back(input[0]); 
    for(int i=1;i<n;i++) 
    {
        for(int j=0;j<i;j++)
        {
            if ((input[j].second < input[i].first) && (dp[j].size() > dp[i].size())) // the condition must be satisfied 
                dp[i] = dp[j];
        } 
        dp[i].push_back(input[i]);
        if(dp[i].size() > dp[mx].size())
        	mx = i;
    }
    for(auto x: dp[mx])
    	cout<<"("<<x.first<<", "<<x.second<<") ";
} 

int main()
{ 
    vector<pair<int,int>> input = {{1, 2}, {10, 30}, {5, 6}, {15, 25}, {17, 21}};
    maxChainLength(input);
}
(1, 2) (5, 6) (10, 30)

Java code to Print Maximum Length Chain of Pairs

import java.util.*;

class Main{
    static void maxChainLength(ArrayList<ArrayList<Integer>> input)
    {
        Collections.sort(input, new Comparator<ArrayList<Integer>> () {
            @Override
            public int compare(ArrayList<Integer> a, ArrayList<Integer> b) {
                return a.get(0).compareTo(b.get(0));
            }
        });

        int n = input.size();
        ArrayList<ArrayList<ArrayList<Integer>>> dp = new ArrayList<ArrayList<ArrayList<Integer>>>();
        for(int i=0;i<n;i++)
            dp.add(new ArrayList<ArrayList<Integer>>());
        int mx = 0;
        // base case
        dp.get(0).add(input.get(0));
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(input.get(j).get(1) < input.get(i).get(0) && (dp.get(j).size() > dp.get(i).size())){
                    dp.set(i, new ArrayList<ArrayList<Integer>>(dp.get(j)));
                }
            }
            dp.get(i).add(input.get(i));
            if(dp.get(i).size() > dp.get(mx).size())
                mx = i;
        }
        for(ArrayList<Integer> x: dp.get(mx))
            System.out.print("("+x.get(0)+", "+x.get(1)+") ");
    }

    public static void main(String[] args)
    {
        ArrayList<ArrayList<Integer>> input = new ArrayList<ArrayList<Integer>>();
        input.add(new ArrayList(Arrays.asList(1, 2)));
        input.add(new ArrayList(Arrays.asList(10, 30)));
        input.add(new ArrayList(Arrays.asList(5, 6)));
        input.add(new ArrayList(Arrays.asList(15, 25)));
        input.add(new ArrayList(Arrays.asList(17, 21)));
        maxChainLength(input);
    }
}
(1, 2) (5, 6) (10, 30)

Complexity Analysis

Time Complexity

O(N^2), because the problem is similar to the LIS problem. And in this problem also we have used a nested loop to find a chain pair such that if we add the current pair. The condition remains satisfied. Thus the time complexity is polynomial.

Space Complexity

O(N^2), the space complexity is also polynomial because we have used vector of vectors. In the worst case when the maximum chain length is equal to the size of the input. Then our vector of vectors will have O(N^2) pairs. Thus space required is also polynomial.

Translate »