Queries on XOR of greatest odd divisor of the range

Problem Statement

The problem “Queries on XOR of greatest odd divisor of the range” states that you are given an array of integer and query q, each query consists of a range. The problem statement asks to find out the XOR of the greatest odd divisor within the given range for each query.

Example

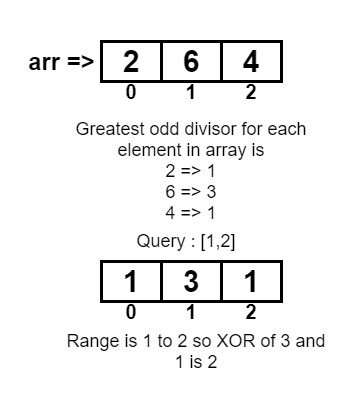
arr[] = {2, 6, 4}
Query :(1, 2), (0, 1)

2 2

Explanation

Greatest odd divisor: (1,3,1)

XOR of 3,1 is 2.

XOR of 1,3 is 2.

Algorithm

1. Traverse the given array.
   1. Keep checking the current element of an array if it is odd and update the current element by the least divisor number.
   2. Set the divArray element to the update element of a given array.
2. Traverse the array again, and update each element of divArray array to the XOR of the current element and previous element of divArray array.
3. Check if the left element is equal to 0, then return the divArray[right].
4. Else return the XOR of divArray[right] and divArray[left-1].

Explanation

We have given an array of integers and some queries to solve. Then we are asked to find out the XOR of the greatest odd divisor. The queries contain two integers. So, it means we have a range within those two integers. For this, first of all, we are going to find all the divisors of each number, while traversing the array. Then we are going to pick up the number from a given array, at a time. We will start a loop for a, particularly given element. In the loop, we will keep on dividing the current element by 2 and update it in the element itself. This thing will go on until the current element is not found to be odd. The time the number will become odd, we break outside the loop.

For each traversal of every element of an array, push the result in divArray array, where it becomes odd. Such that there will be an equal element in an array as there are in a given array. But all of the divisors are there in the divArray. After the completion of the array, traverse the array in which all the divisors are stored. Thus, the divArray array which is storing all the values is the divisors. Then we are going to perform the XOR operation on the divArray values. We are going to traverse the divArray, and XOR the current element and the previous element of the array. And this thing should be done till the operation performed on each pair as the current and previous value.

So, when we are given a query as a range, left, and right. Then we are going to check if the left is equal to zero. Then return divArray[right], else we are going to return the XOR of divArray[right] and divArray[left-1].

Code

C++ code to answer queries on XOR of greatest odd divisor of the range

#include<iostream>

using namespace std;

void getDivisorArray(int arr[], int divArray[], int n)
{
    for (int i = 0; i < n; i++)
    {
        while (arr[i] % 2 != 1)
            arr[i] /= 2;

        divArray[i] = arr[i];
    }
    for (int i = 1; i < n; i++)
        divArray[i] = divArray[i - 1] ^ divArray[i];
}

int solveQuery(int divArray[], int left, int right)
{
    if (left == 0)
        return divArray[right];
    else
        return divArray[right] ^ divArray[left - 1];
}

int main()
{
    int arr[] = {2, 6, 4};
    int n = sizeof(arr) / sizeof(arr[0]);

    int divArray[n];
    getDivisorArray(arr, divArray, n);

    cout << solveQuery(divArray, 1, 2) << endl;
    cout << solveQuery(divArray, 0, 1) << endl;

    return 0;
}

2
2

Java code to answer Queries on XOR of greatest odd divisor of the range

class QueriesXOR
{
    public static void getDivisorArray(int arr[], int divArray[], int n)
    {
        for (int i = 0; i < n; i++)
        {
            while (arr[i] % 2 != 1)
                arr[i] /= 2;

            divArray[i] = arr[i];
        }
        for (int i = 1; i < n; i++)
            divArray[i] = divArray[i - 1] ^ divArray[i];
    }
    
    static int solveQuery(int divArray[], int l, int r)
    {
        if (l == 0)
            return divArray[r];
        else
            return divArray[r] ^ divArray[l - 1];
    }
    
    public static void main (String[] args)
    {
        int arr[] = {2, 6, 4};
        int n = arr.length;

        int divArray[] = new int[n];
        getDivisorArray(arr, divArray, n);

        System.out.println(solveQuery(divArray, 1, 2)) ;
        System.out.println (solveQuery(divArray, 0, 1));
    }
}

2
2

Complexity Analysis

Time Complexity

O(N log n) where “N” is the number of elements in the array. And n is the number present in the array log has base 2. The log n factor is because of the division of number until we get an odd divisor.

Space Complexity

O(N) where “N” is the number of elements in the array. We have used an array to store the xor values which is taking the space.