Floyd Warshall Algorithm

Difficulty Level Medium
Frequently asked in Samsung
Dynamic Programming Graph Shortest PathViews 5028

Floyd Warshall Algorithm is a method to find the shortest path between two vertices for all the pairs of vertices. We apply this method to a weighted graph with no negative cycles. We apply some operations to the V*V matrices which initially store large value(infinite) in each cell. Here we use the Dynamic Programming approach to find the shortest path between all the possible pairs of vertices in a given graph. We solve this problem by taking a sequence of decisions. Let’s understand this by an example.

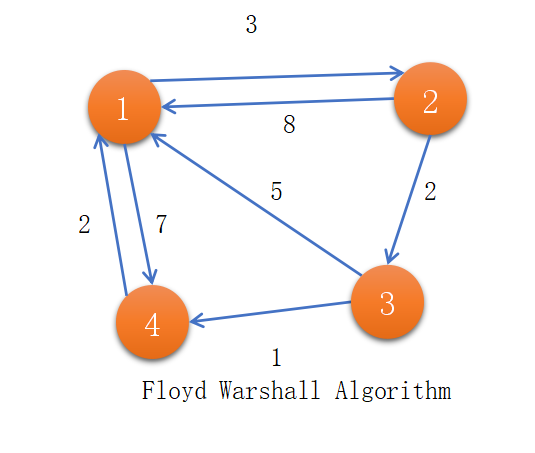
Floyd Warshall Algorithm

Working of Floyd Warshall Algorithm

Step-1

Make a matrix A0 which stores the information about the minimum distance of path between the direct path for every pair of vertices. If there is no edge between two vertices, then we initialize the distance of path in that case as infinity(very big number). See all the steps on the bases of the above-directed graph.

Floyd Warshall Algorithm

Step-2

In this step, we use Ao matrix and find the shortest path via 1 as an intermediate node. Here all the path that belongs to 1 remain unchanged in the matrix A1. Here one more thing which is important, there is no self-loop so the diagonals are 0 always.

A1[1,1]=0, A1[2,2]=0, A1[3,3]=0, A1[4,4]=0.

A1[1,2], A1[1,3], A1[1,4], A1[2,1], A1[3,1], A1[4,1] are remain same as in matrix A0.

A1[2,3]= min(A0[2,3], A0[2,1]+A0[1,3]) = Infinity.

A1[2,4]= min(A0[2,4], A0[2,1]+A0[1,4]) = 15. Similarly find the others values. Final matrix A1 is look like:

Floyd Warshall Algorithm

Step-3 

In this step, we use A1 matrix and find the shortest path via 2 as an intermediate node. Here all the path that belongs to 2 remain unchanged in the matrix A2. Here one more thing which is important, there is no self-loop so the diagonals are 0 always.

A2[1,1]=0, A2[2,2]=0, A2[3,3]=0, A2[4,4]=0.

A2[1,2], A2[3,2], A2[4,2], A2[2,1], A2[2,3], A2[2,4] are remain same as in matrix A1.

A2[1,3]= min(A1[1,3], A1[1,2]+A1[2,3]) = 5.

A2[1,4]= min(A1[1,4], A1[1,2]+A1[2,4]) = 7. Similarly find the others values. Final matrix A2 is look like:

Step-4 

In this step, we use A2 matrix and find the shortest path via 3 as an intermediate node. Here all the path that belongs to 3 remain unchanged in the matrix A3. Here one more thing which is important, there is no self-loop so the diagonals are 0 always.

A3[1,1]=0, A3[2,2]=0, A3[3,3]=0, A3[4,4]=0.

A3[1,3], A3[2,3], A3[4,3], A3[3,1], A3[3,2], A3[3,4] are remain same as in matrix A2.

A3[1,2]= min(A2[1,2], A2[1,3]+A2[3,2]) = 3.

A3[1,4]= min(A2[1,4], A2[1,3]+A2[3,4]) = 6. Similarly find the others values. Final matrix A3 is look like:

Step-5 

In this step, we use A3 matrix and find the shortest path via 4 as an intermediate node. Here all the path that belongs to 4 remain unchanged in the matrix A4. Here one more thing which is important, there is no self-loop so the diagonals are 0 always.

A4[1,1]=0, A4[2,2]=0, A4[3,3]=0, A4[4,4]=0.

A4[1,4], A4[2,4], A4[3,4], A4[4,1], A4[4,2], A4[4,3] are remain same as in matrix A3.

A4[1,2]= min(A3[1,2], A3[1,4]+A3[4,2]) = 3.

A4[1,3]= min(A3[1,3], A3[1,4]+A3[4,3]) = 5. Similarly find the others values. Final matrix A4 is look like:

A4 matrix is our final matrix which tells us the minimum distance between two vertices for all the pairs of vertices.

Algorithm For Floyd Warshall Algorithm

Step:1 Create a matrix A of order N*N where N is the number of vertices.
Step:2 For i in range 1 to N:
       i) For j in range 1 to N:
          a) For k in range 1 to N:
             A^(k)[j,k]= MIN(A^(k-1)[j,k],A^(k-1)[j,i]+A^(K-1)[i,k]).
Step:3 Print the array A.

Implementation For Floyd Warshall Algorithm

/*C++ Implementation of Floyd Warshall Algorithm.*/ 
#include<bits/stdc++.h> 
using namespace std; 
#define INF 1000000009
int main() 
{
    /*input values*/
    int nodes,edges;
    cin>>nodes>>edges;
    int a[nodes+1][nodes+1];
    memset(a,INF,sizeof(a));
    /*create matrix A0*/
    for(int i=0;i<edges;i++)
    {
        int x,y,weight;
        cin>>x>>y>>weight;
        a[x][y]=weight;
    }
    /*All the diagonals values are 0*/
    for(int i=1;i<=nodes;i++)
    {
        a[i][i]=0;
    }
    /*find the final matrix A^n*/
    for(int i=1;i<=nodes;i++)
    {
        for(int j=1;j<=nodes;j++)
        {
            for(int k=1;k<=nodes;k++)
            {
                a[j][k]=min(a[j][k],a[j][i]+a[i][k]);
            }
        }
    }
    /*Print the answer(final matrix)*/
    for(int j=1;j<=nodes;j++)
    {
        for(int k=1;k<=nodes;k++)
        {
            cout<<a[j][k]<<" ";
        }
        cout<<endl;
    }
    return 0;
}
4 7
1 2 3
2 1 8
2 3 2
3 4 1
4 1 2
1 4 7
0 3 5 6 
5 0 2 3 
3 6 0 1 
2 5 7 0

Time Complexity

O(N*N*N) where N is the number of nodes in the given graph. Here we handle the N*N matrix N times so for the overall operation to get the final matrix we run 3 nested loops.

Space Complexity

O(N*N) where N is the number of nodes in the given graph. We handle a matrix of order N*N to get the final result of the algorithm.

References

Translate »