Given two unsorted arrays find all pairs whose sum is x

Difficulty Level Easy
Frequently asked in Amazon Facebook
Array Hash HashingViews 4702

Problem Statement

Given two unsorted arrays, find all pairs whose sum is x problem states that you are given two arrays of integers that are unsorted and a value called sum. The problem statement asks to find out the total number of pairs and print all those pairs that add up to the given value called sum.

Example

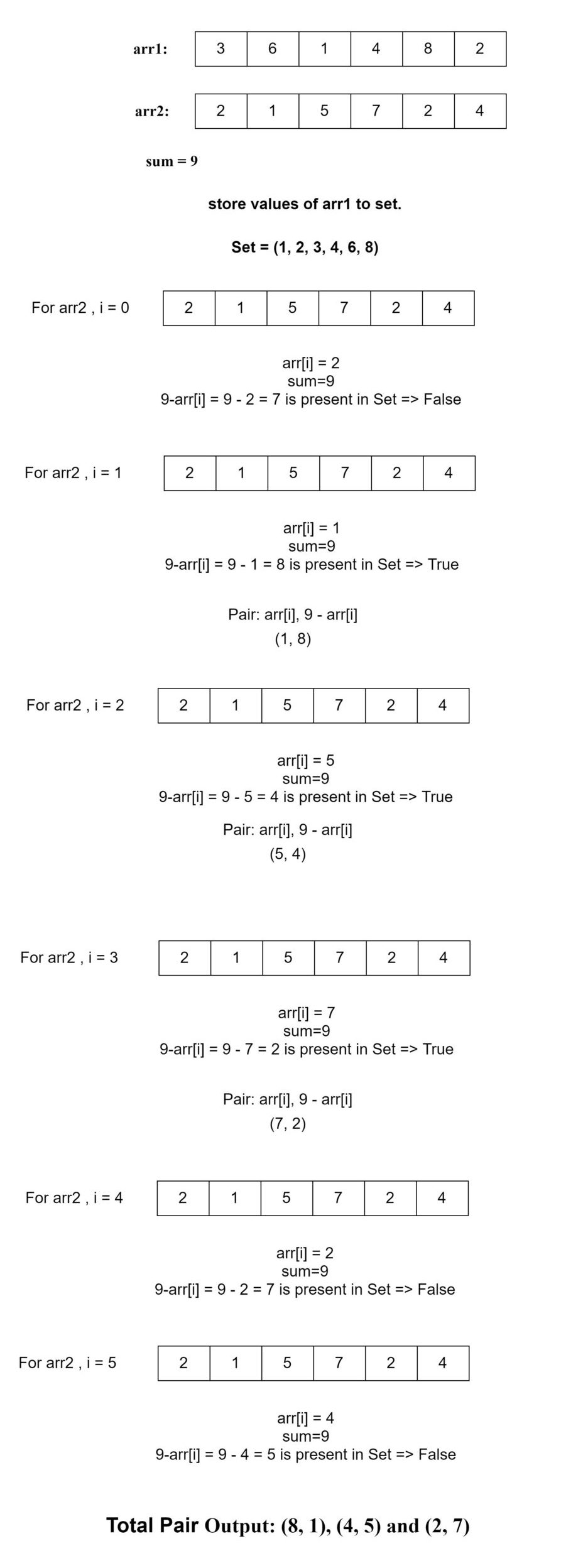
arr1[] = { 3,6,1,4,8,2}

arr2[] = { 2,1,5,7,2,4}

sum = 9
(8, 1), (4, 5) (2, 7)

Explanation: All three pairs have a number that has the sum equal to the given value 9.

arr1[] = { 2,5,1,7,9}

arr2[] = { 3,6,8,1,0}

sum = 7
(1, 6), (7, 0)

Explanation: Both two pairs have a number that has the sum equal to the given value 7.

Algorithm to find all pairs having sum = x in two unsorted arrays

1. Declare a Set.
2. Insert all the values of array1 into the Set.
3. Traverse the array2.
4. Check if the difference of sum and each number of array2 is present in a set.
5. If present then prints the difference and the current array element.

Explanation

Given two unsorted arrays, find all pairs whose sum is x. For this, we are going to use the set. A set provides also a feature of removing the common elements. What we are going to do is we will insert all the values of array1 into the set. Here, if set removes or does not remove the elements. We do not care about that much because we only need the number to check if the pair can be formed.

While traversing the first array, we will be inserting all the values of it into the set. Later, with this set, we will find if we have any pair that can be formed whose sum is equal to the given value called sum. When we finished with inserting all the values into the set, we will traverse the array 2.

Starting for the first element of the second array we will check for the difference of the given value and each value of the second array while traversing. It is a similar thing as we can add two numbers say a + b = c, and now if we have only b and c, with c-b we can find out the ‘a’. The same thing is here we have the resultant value we can find out which value is required to complete the pair. That’s why we are looking for a difference of sum and each value of array2 in array1. If we find the pairs simply print the difference of the pair and the current array element, this will be the required pair.

Given two unsorted arrays, find all pairs whose sum is x

Code

C++ code to find all pairs having sum = x in two unsorted arrays

#include<iostream>
#include<unordered_set>

using namespace std;

void getPairsofSum(int arr1[], int arr2[], int l1, int l2, int sum)
{
    unordered_set<int> MAP;
    for (int i = 0; i < l1; i++)
        MAP.insert(arr1[i]);

    for (int j = 0; j < l2; j++)
        if (MAP.find(sum - arr2[j]) != MAP.end())
            cout << sum - arr2[j] << " "<< arr2[j] << endl;
}
int main()
{
    int arr1[] = { 3,6,1,4,8,2};
    int arr2[] = { 2,1,5,7,2,4};
    int sum = 9;
    int l1 = sizeof(arr1) / sizeof(int);
    int l2 = sizeof(arr2) / sizeof(int);
    getPairsofSum(arr1, arr2, l1, l2, sum);
    return 0;
}

8 1
4 5
2 7

 

Java code to find all pairs having sum = x in two unsorted arrays

import java.util.HashMap;

class PairofSumUnsortedArray
{
    public static void getPairsofSum(int arr1[], int arr2[], int l1, int l2, int sum)
    {
        HashMap<Integer, Integer> MAP = new HashMap<Integer, Integer>();

        for (int i = 0; i < l1; i++)
            MAP.put(arr1[i], 0);

        for (int j = 0; j < l2; j++)
            if (MAP.containsKey(sum - arr2[j]))
                System.out.println(sum - arr2[j] + " " + arr2[j]);
    }
    public static void main(String[] args)
    {
        int arr1[] = { 3,6,1,4,8,2};
        int arr2[] = { 2,1,5,7,2,4};
        int sum = 9;
        getPairsofSum(arr1, arr2, arr1.length, arr2.length, sum);
    }
}

8 1
4 5
2 7

 

Complexity Analysis

Time complexity

O(max(n, m)) where “n” and “m” is the length of the first and second array.

Space Complexity

O(max(n, m)) where “n” and “m” is the length of the first and second array.

Translate »