Subarrays with distinct elements

Difficulty Level Medium
Frequently asked in Cisco FreeCharge Times Internet Zoho
Array Hash HashingViews 4856

Problem Statement

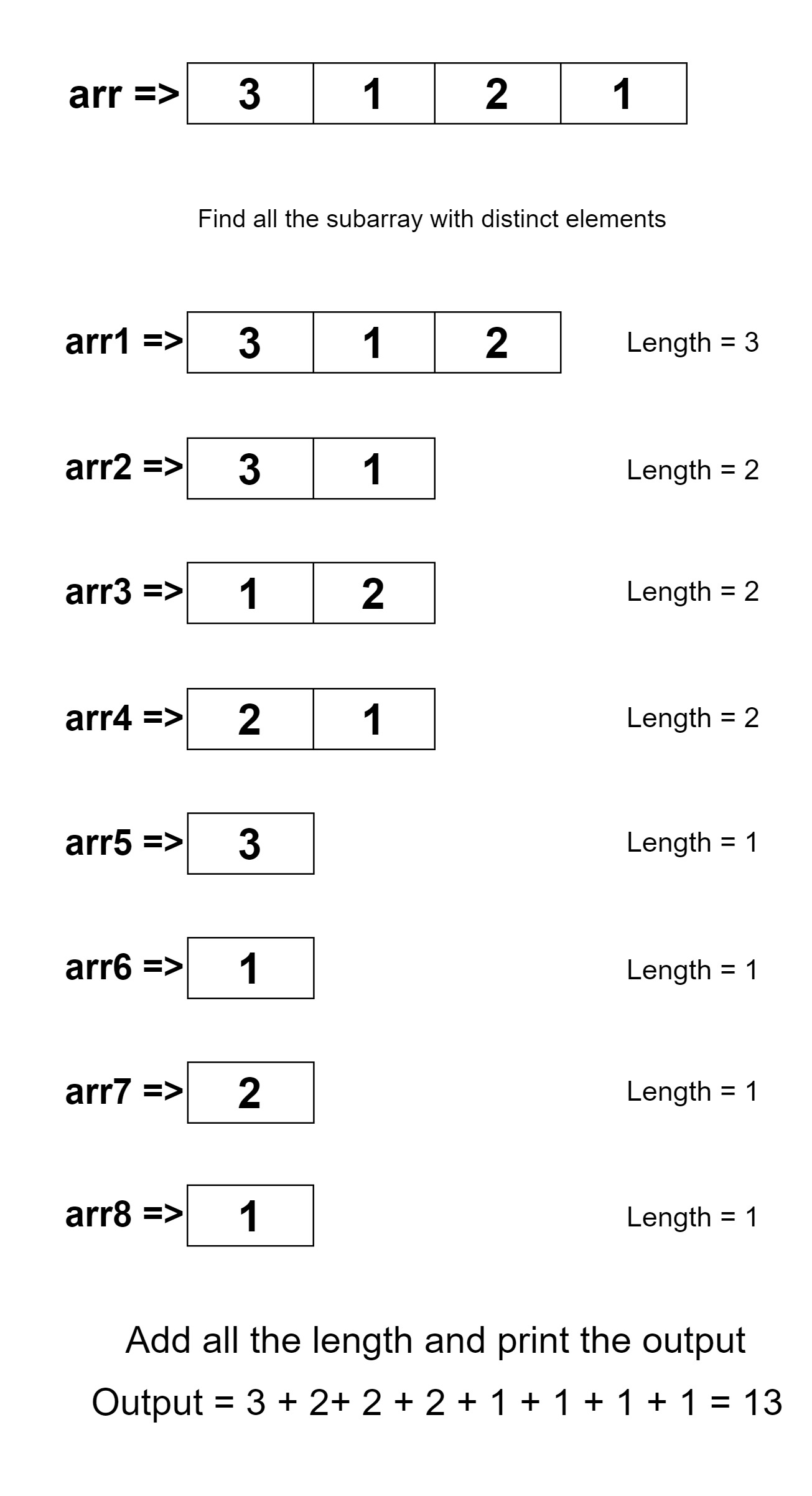
“Subarrays with distinct elements” states that you are given an array of integer elements. The problem statement asks to find the sum of lengths of contiguous sub-arrays that are having all elements different from each other.

Example

arr[] = {3, 1, 2, 1}
4

Explanation: The sub-arrays are ⇒ (3, 1, 2), (3, 1), (1, 2), (2,1), (3), (1), (2), (1)

Total length of all the elements are (3 + 2 + 2 + 2 + 1 + 1 + 1 + 1) = 10.

Subarrays with distinct elements

arr[] = {3, 5, 8, 9}
20

Explanation: The sub-arrays are ⇒ (3), (5), (8), (9), (3, 5), (5, 8), (8, 9), (3, 5, 8), (5, 8, 9), (3, 5, 8, 9)

Total length of all the elements are (1 + 1 + 1 + 1 + 2 + 2 + 2 +3 +3 +4) = 10.

Algorithm to find Subarrays with distinct elements

1. Declare a map.
2. Set output and j to 0.
3. Traverse the array from i=0 to i<n(length of an array).
  1. While j is less than n and if a set doesn’t contain the value of arr[j].
    1. Insert all the values of arr [j].
  2. Update the output to output +=((j - i) * (j - i + 1))/2.
  3. Remove the arr[i] from Set.
4. Return output.

Explanation

We have given an integer array. Our task is to find out the sum of the length of all the sub-arrays that are contiguous and only have distinct elements. We will use a Set. Set provides a feature of removal of copied or common elements from a Set. Set j to 0 and output to 0.

Start by traversing the array and use a while loop. Set the value of j to 0 and inside while loop we gonna traverses the loop while incrementing j. Set some conditions on it, while j is less than n, i.e, the length of the array and also if it is found that Set contains the value of arr[j]. Let us consider an example:

Arr[]={3, 1, 2, 1}

We will be traversing the array picking each element at one time, suppose we will select 3 at the first time, in arr[j], idea is to keep the outer loop constant just for a while this 3 will start in while loop, as j is initialized as 0, and set doesn’t contain 3 for the first time, so it will enter in a while loop and insert the arr[j] means 3 and increase the j++, It will pick next element as 1, Set doesn’t contain it so it will be inserted in a set, then comes 2 and then comes 1, but this time, 1 is already in the loop so it will come out to of the while loop.

Now when we come out of the loop we have incremented value of j, so we will update the output according to that. And for further traversal, we need to remove the array’s element, so that we can find out the possible length of the sum of distinct elements in sub-array. And finally, we will return that output.

Code

C++ to find subarrays with distinct elements

#include<iostream>
#include<unordered_set>

using namespace std;

int getLength(int arr[], int n)
{
    unordered_set<int> SET;

    int j = 0, output = 0;
    for (int i=0; i<n; i++)
    {
        while (j < n && SET.find(arr[j]) == SET.end())
        {
            SET.insert(arr[j]);
            j++;
        }
        output += ((j - i) * (j - i + 1))/2;
        SET.erase(arr[i]);
    }
    return output;
}
int main()
{
    int arr[] = {3, 1, 2, 1};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << getLength(arr, n);
    return 0;
}

13

Java code to find subarrays with distinct elements

import java.util.Set;
import java.util.HashSet;

class LengthOfDistinctElements
{
    public static int getLength(int[] arr, int n)
    {
        Set<Integer> SET = new HashSet<>();
        int j = 0, output = 0;
        for (int i = 0; i < n; i++)
        {
            while (j < n && !SET.contains(arr[j]))
            {
                SET.add(arr[j]);
                j++;
            }
            output += ((j - i) * (j - i + 1)) / 2;
            SET.remove(arr[i]);
        }
        return output;
    }
    public static void main(String[] args)
    {
        int[] arr = { 3, 1, 2,1  };
        int n = arr.length;
        System.out.println(getLength(arr, n));
    }
}

13

Complexity Analysis

Time Complexity

We have been traversing the array, and using HashSet allows performing insertion and other such operations in O(1). Thus we achieve O(N) time complexity where “N” is the number of elements in the array.

Space Complexity

Since we stored only N elements, we achieved linear space complexity. O(N) where “N” is the number of elements in the array

Translate »