N queen problem using the concept of Backtracking. Here we place queen such that no queen under attack condition. The attack condition of the queens is if two queens are on the same column, row, and diagonal then they are under attack. Let’s see this by the below figure.
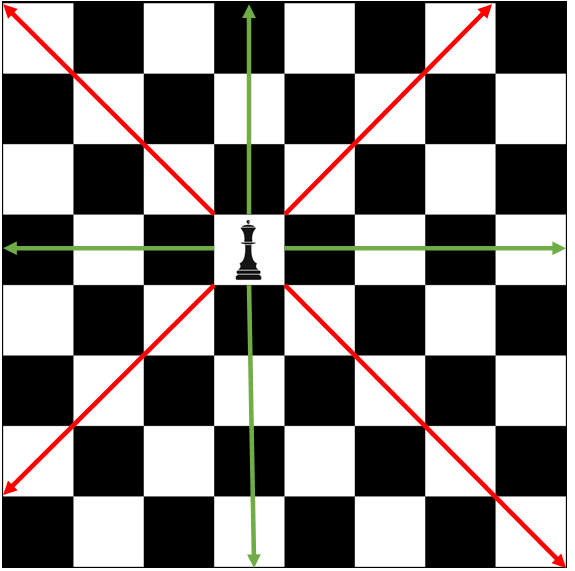
Here we see that the position of the queen is at 4th row and 4th column from the topmost left side. If we put another queen on the cells where the red line is drawn then, that queen is under attack. This is the case of the same diagonals. If we put another queen on the cells where the green line is drawn then, that queen is under attack, and in this is the case of the same row and column.
So, in this problem, we have to place N queens on the N*N chessboard such that no queens are under attack conditions.
Table of Contents
Input Format
First-line containing single integer value N.
Output Format
Print N*N matrix where cell value is 1 if the queen is present in that cell otherwise 0.
Explanation For N queen problem
Here firstly we put one queen in the ith row and the ith column where 1<=i<=N. Let’s see the 4 Q problem for understanding.

Now, we see that only the queens are under attack along diagonals. So, we check that how to place N-i th queen in N-i th row such that it’s in a safe zone where 0<=i<=n-1. Here we can’t place 2nd queen in (2,2) cell so, keep it in (2,3) cell. Then we change the position of the 3rd queen to (2,3) cell.

Now, we see that there is no position to store 3rd queen in the safe zone so we directly change the position of queen 2 without going to 4th queen. And remember that no two queens come on the same column.

Here, we see that we can’t have an option to store the 4th queen in safe zone. For 1 queen at (1,1) we check all the possible cases and we still don’t get our solution. So, change the position of 1st queen to (1,2) and 2nd queen to (2,1) in starting condition where we place N queens. Then one possible way is:

Now, we see that the 2nd queen is under attack then we change the position of 2nd queen to (2,4). Two queens newer in the same column so we change the position of 4th queen to (1,4).

In this case, the 3rd queen is under attack condition so we change the position of 2nd queen to (3,1). Two queens newer in the same column so we change the position of 4th queen to (4,3).

In this case no queen in under attack condition so, we directly print our answer. Where the queen is present in a cell then we print 1 otherwise 0. For this example see the input/output format.
Example Input: 4
Example Output: 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0
Algorithm Used For N queen problem
Step:1 Set all queens such that ith queen place on (i, i) cell.
Step:2 For j in range j to N:
i) Check for all the possible values of the jth row.
ii) Change the position of queens such that no queens come in the same column.
iii) If the jth queen is placed on its right place, see other queens for that position.
iv) If all queens are placed such that no queens are under attack then print the result.Implementation For N queen problem
/*C++ Implementation for N-QUEUE PROBLEM*/
#include<bits/stdc++.h>
using namespace std;
const int maxsize=1000;
int valid(int chess_board[][maxsize],int row, int column, int n)
{
/*check for whether there is two queen on the same raw*/
for(int i=0;i<column;i++)
{
if(chess_board[row][i])
{
return 0;
}
}
/*check whether there is a queen on the left upper diagonal*/
for(int i=row,j=column;i>=0&&j>=0;i--,j--)
{
if(chess_board[i][j])
{
return 0;
}
}
/*check whether there is a queen on the left bottom diagonal*/
for(int i=row,j=column;i<n&&j>=0;i++,j--)
{
if(chess_board[i][j])
{
return 0;
}
}
/*if queen in safe condition*/
return 1;
}
int solution_existency(int chess_board[][maxsize],int column,int n)
{
/*if n queens are placed successfully*/
if(column>=n)
{
return 1;
}
/*for each row check placing of queen is possible or not*/
for(int i=0;i<n;i++)
{
if(valid(chess_board,i,column,n))
{
/*if its valid position then place at here(i,column)*/
chess_board[i][column]=1;
if(solution_existency(chess_board,column+1,n))
{
return 1;
}
/*where no place is possible to place the queen then remove the queen*/
chess_board[i][column]=0;
}
}
/*when no case found in which we store n queens in chess board*/
return 0;
}
int n_queen(int chess_board[][maxsize], int n)
{
int i=solution_existency(chess_board,0,n);
return i;
}
int main()
{
int n;
/*input value*/
cin>>n;
int chess_board[maxsize][maxsize];
memset(chess_board,0,sizeof(chess_board));
int possible=n_queen(chess_board,n);
if(possible)
{
/*Print the chess board current state which is our answer*/
cout<<"Chess board current state: "<<endl;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout<<chess_board[i][j]<<" ";
}
cout<<'\n';
}
}
else
{
cout<<-1<<endl;
}
return 0;
}8
Chess board current state: 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0
Time Complexity
O(N*N*N) which is maximum possible when we check the possible valid position of each queen in N*N Chessboard and O(N) time for check the valid position of the queue after each queen position.
Space Complexity
O(N*N) where N is the one side of the chessboard. We use a N*N matrix to store the position of the queen to perform the operation for finding the valid position of each queen.