Table of Contents
Problem Statement
The problem “First negative integer in every window of size k” states that you are given an array containing positive and negative integers, for every window of size k print the first negative integer in that window. If there is no negative integer in any window then output 0(zero).
Examples
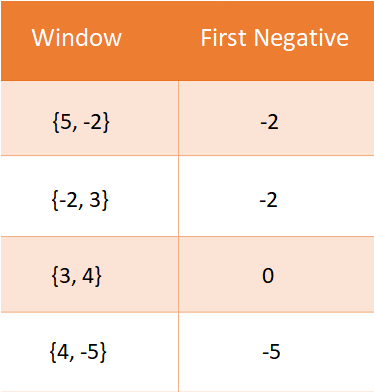
arr[] = {5, -2, 3, 4, -5}
k = 2-2 -2 0 -5
arr[] = {7, 9, -1, 2, 3, 4, -2, -3, -4}
k = 3-1 -1 -1 0 -2 -2 -2
Naive Approach
For every window of size k, traverse through all the elements of the window and print the first negative integer.
- Run a loop for i equals 0 to (n – k), here each i corresponds to a window of size k.
- Run a nested loop for j equals i to (i + k)(not included). This loop traverses the window i.
- If the value of arr[j] is negative print it and break, else continue to check for the next element.
- If there is no negative element in a window, print 0.
Complexity Analysis
Time Complexity = O(n * k)
Space Complexity = O(1)
where n is the number of elements in the given array.
Since we are solving the problem independently for each window of size k, we are traversing through n*k elements in general. And thus polynomial time complexity. And since we haven’t stored anything the space complexity is constant.
Java Code to find first First negative integer in every window of size k
class FirstNegativeIntegerInEveryWindowOfSizeK {
private static void firstNegativeInteger(int[] arr, int k) {
int n = arr.length;
// Run a loop corresponding to every window in the array
for (int i = 0; i <= n - k; i++) {
boolean negFound = false;
// Traverse the window
for (int j = i; j < i + k; j++) {
// If current element if negative print it
if (arr[j] < 0) {
System.out.print(arr[j] + " ");
negFound = true;
break;
}
}
// if there is no negative element then print 0
if (!negFound)
System.out.print("0 ");
}
System.out.println();
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{5, -2, 3, 4, -5};
int k1 = 2;
firstNegativeInteger(arr1, k1);
// Example 2
int arr2[] = new int[]{7, 9, -1, 2, 3, 4, -2, -3, -4};
int k2 = 3;
firstNegativeInteger(arr2, k2);
}
}-2 -2 0 -5 -1 -1 -1 0 -2 -2 -2
C++ Code to find First negative integer in every window of size k
#include<bits/stdc++.h>
using namespace std;
void firstNegativeInteger(int *arr, int k, int n) {
// Run a loop corresponding to every window in the array
for (int i = 0; i <= n - k; i++) {
bool negFound = false;
// Traverse the window
for (int j = i; j < i + k; j++) {
// If current element if negative print it
if (arr[j] < 0) {
cout<<arr[j]<<" ";
negFound = true;
break;
}
}
// if there is no negative element then print 0
if (!negFound)
cout<<"0 ";
}
cout<<endl;
}
int main() {
// Example 1
int arr1[] = {5, -2, 3, 4, -5};
int k1 = 2;
firstNegativeInteger(arr1, k1, sizeof(arr1) / sizeof(arr1[0]));
// Example 2
int arr2[] = {7, 9, -1, 2, 3, 4, -2, -3, -4};
int k2 = 3;
firstNegativeInteger(arr2, k2, sizeof(arr2) / sizeof(arr2[0]));
}-2 -2 0 -5 -1 -1 -1 0 -2 -2 -2
Optimal Approach
The optimal approach to solve above problem is to use a Deque and sliding window technique. The Deque stores the indexes of negative elements in a window. The first element of the Deque corresponds to the index of first negative element in the window. While changing the window, remove the previous window element from the Deque and also add the new element to the Deque. If the Deque is empty while checking for the first negative element, print 0.
- Create a Deque q. Consider the first window of size k.
- Traverse the elements of the first window, if the element is negative, push its index to the end of the Deque.
- At the end of the traversal if the Deque is empty print 0, else the first element in the Deque corresponds to the index of first negative element.
- Traverse in the remaining array(start from index k to n – 1), while the front of Deque is less than (i – k) remove it. If the current element is negative, add it to Deque.
- The first element in the Deque corresponds to the first negative element for this window, if the Deque is empty there is no negative element in this window, print 0.
Complexity Analysis
Time Complexity = O(n)
Space Complexity = O(n)
where n is the number of elements in the given array.
Here, because we have used a queue, the space complexity is linear. As for the time complexity, we have simply traversed through all the elements of the input. Thus time complexity is also linear.
Java Code to find First negative integer in every window of size k
import java.util.Deque;
import java.util.LinkedList;
class FirstNegativeIntegerInEveryWindowOfSizeK {
private static void firstNegativeInteger(int[] arr, int k) {
int n = arr.length;
// create a deque q
Deque<Integer> q = new LinkedList<>();
// traverse the first window
for (int i = 0; i < k; i++) {
// if the current element is negative add it to the end of deque
if (arr[i] < 0)
q.addLast(i);
}
// if deque is not empty, front of deque is the index of first negative element
// else there is no negative element in this window
if (!q.isEmpty())
System.out.print(arr[q.peek()] + " ");
else
System.out.print("0 ");
for (int i = k; i < n; i++) {
// remove previous window elements
while (!q.isEmpty() && q.peek() <= (i - k)) {
q.removeFirst();
}
// if the current element is negative, add it to the deque
if (arr[i] < 0)
q.addLast(i);
// if deque is not empty, front of deque is the index of first negative element
// else there is no negative element in this window
if (!q.isEmpty())
System.out.print(arr[q.peek()] + " ");
else
System.out.print("0 ");
}
System.out.println();
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{5, -2, 3, 4, -5};
int k1 = 2;
firstNegativeInteger(arr1, k1);
// Example 2
int arr2[] = new int[]{7, 9, -1, 2, 3, 4, -2, -3, -4};
int k2 = 3;
firstNegativeInteger(arr2, k2);
}
}-2 -2 0 -5 -1 -1 -1 0 -2 -2 -2
C++ Code to find First negative integer in every window of size k
#include<bits/stdc++.h>
using namespace std;
void firstNegativeInteger(int *arr, int k, int n) {
// create a deque q
deque<int> q;
// traverse the first window
for (int i = 0; i < k; i++) {
// if the current element is negative add it to the end of deque
if (arr[i] < 0)
q.push_back(i);
}
// if deque is not empty, front of deque is the index of first negative element
// else there is no negative element in this window
if (!q.empty())
cout<<arr[q.front()]<<" ";
else
cout<<"0 ";
for (int i = k; i < n; i++) {
// remove previous window elements
while (!q.empty() && q.front() <= (i - k)) {
q.pop_front();
}
// if the current element is negative, add it to the deque
if (arr[i] < 0)
q.push_back(i);
// if deque is not empty, front of deque is the index of first negative element
// else there is no negative element in this window
if (!q.empty())
cout<<arr[q.front()]<<" ";
else
cout<<"0 ";
}
cout<<endl;
}
int main() {
// Example 1
int arr1[] = {5, -2, 3, 4, -5};
int k1 = 2;
firstNegativeInteger(arr1, k1, sizeof(arr1) / sizeof(arr1[0]));
// Example 2
int arr2[] = {7, 9, -1, 2, 3, 4, -2, -3, -4};
int k2 = 3;
firstNegativeInteger(arr2, k2, sizeof(arr2) / sizeof(arr2[0]));
}-2 -2 0 -5 -1 -1 -1 0 -2 -2 -2