Priority Queue in C++

FIFO manner is used to implement a queue. In a queue, insertions are done at one end (rear) and deletion takes place at another end (front). Basically, the element enters first is deleted first. We implement a priority queue using c++ inbuilt functions.

Characteristics of Priority Queue

1. A priority queue is an extension of a simple queue.
2. In the priority queue, the elements do not follow FIFO.
3. In priority queue on the basis of priority elements are deleted.
4. Every element in the priority queue has a priority assigned to it.
5. On the basis of that priority, elements are removed from the priority queue.
6. The element with the highest priority is always at the top of the queue.
7. Element with the lowest priority is always at the lowest of the queue

Syntax

priority_queue <int> pq;

Example

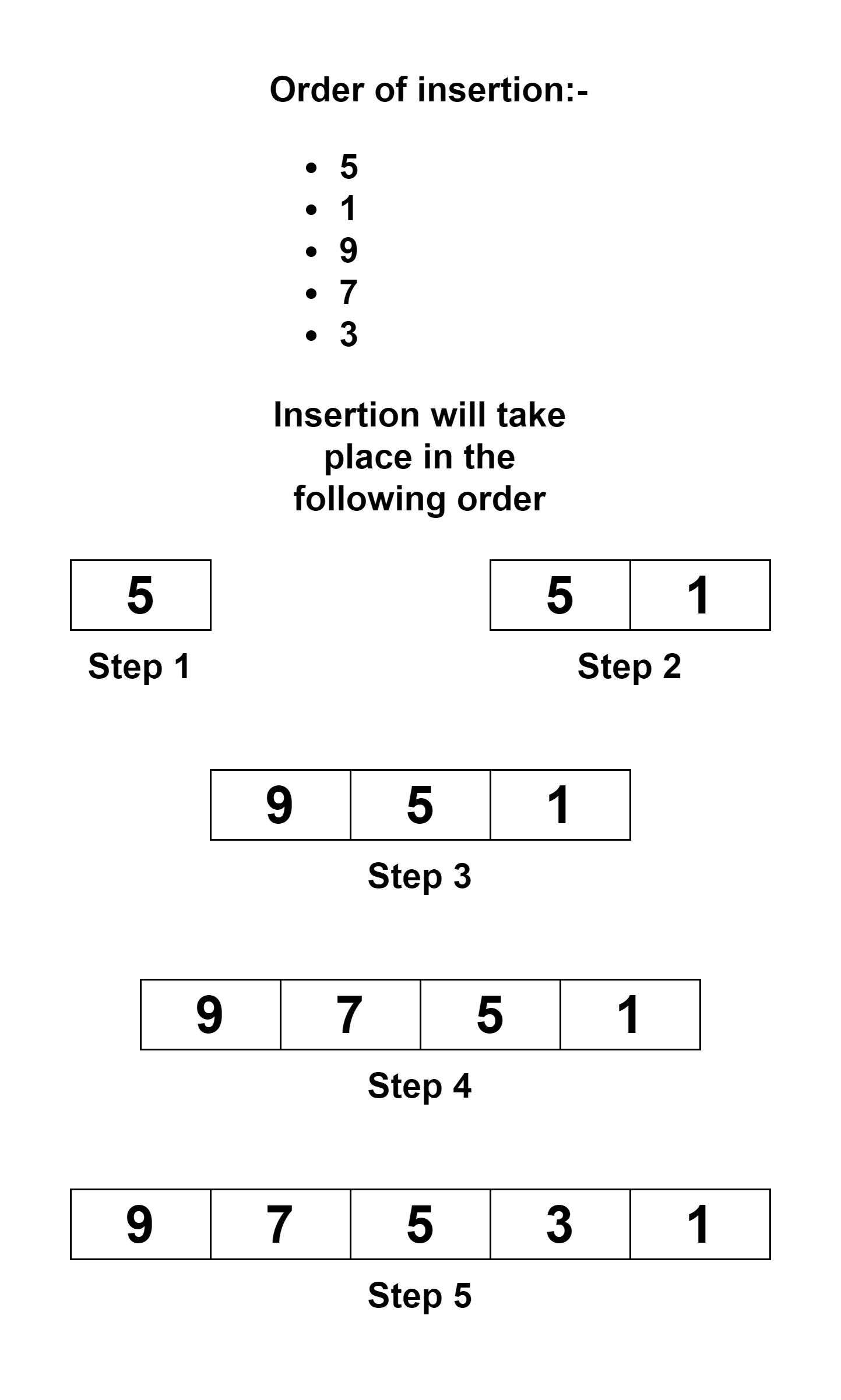
Input

5,1,9,7,3

Output

9,7,5,3,1

Functions of Priority Queue

A priority queue in C++ supports various functions. Some of the functions are described below:

1. push(): Insert an element in the queue.
2. pop(): Delete the lowest priority element from the queue.
3. size(): the length of the priority queue is returned.
4. empty(): if the priority queue is empty return true else returns false.
5. top(): highest priority element is returned.
6. swap(): Copies the element to another priority queue of similar size and type.
7. emplace(): Inserts an element in the priority queue at the top.

Implementation

Implementation of priority queue is possible using various data structures such as an array, linked list, or heap. The most efficient and simple way to implement a priority queue is by using a heap. Heaps are preferred over any other data structure because heaps provide better performance than other data structures.

In C++ we are provided a stl library for priority queue which can be used easily to implement a priority queue.

#include <iostream>
#include <queue>
#include<stdlib.h>

using namespace std;

int pq_display(priority_queue <int> pq);

int main ()
{
    priority_queue <int> pq;
    int num, choice;
    cout <<" 1 - Insert an element into queue" <<endl;
    cout <<" 2 - Delete first element from queue" <<endl;
    cout <<" 3 - Display queue elements" <<endl;
    cout <<" 4 - Display highest priority queue element" <<endl;
    cout <<" 5 - Exit" <<endl;
    while (1)
    {
        cout <<endl<< "Enter your choice : ";
        cin >> choice;
        switch (choice)
        {
        case 1:
            cout << "Enter value to be inserted : ";
            cin >> num;
            pq.push(num);
            break;
        case 2:
            cout << "The first element " << pq.top() <<" has been removed from the queue" <<endl;
            pq.pop();
            break;
        case 3:
            pq_display(pq);
            break;
        case 4:
            cout <<"The highest priority element in the queue is " << pq.top() <<endl;
            break;
        case 5:
            exit(0);
        default:
            cout << "Choice is incorrect, Enter a correct choice";
        }
    }
    return 0;
}

int pq_display(priority_queue <int> pq)
{
    while (!pq.empty())
    {
        cout <<pq.top() <<'\t' ;
        pq.pop();
    }
    cout << '\n';
    return 0;
}

 1 - Insert an element into queue
 2 - Delete first element from queue
 3 - Display queue elements
 4 - Display highest priority queue element
 5 - Exit

Enter your choice : 1
Enter value to be inserted : 9

Enter your choice : 1
Enter value to be inserted : 7

Enter your choice : 1
Enter value to be inserted : 5

Enter your choice : 1
Enter value to be inserted : 3

Enter your choice : 1
Enter value to be inserted : 1

Enter your choice : 3
9       7       5       3       1

Complexity Analysis of Priority Queue using C++

Time Complexity

O(N * log(n)) where “N” is the number of insertions and deletions performed and “n” is the size of the priority queue.

Space Complexity

O(n) where “n” is the number of elements in the priority queue.

References