Topological Sorting

Given a directed acyclic graph, topologically sort the graph nodes.

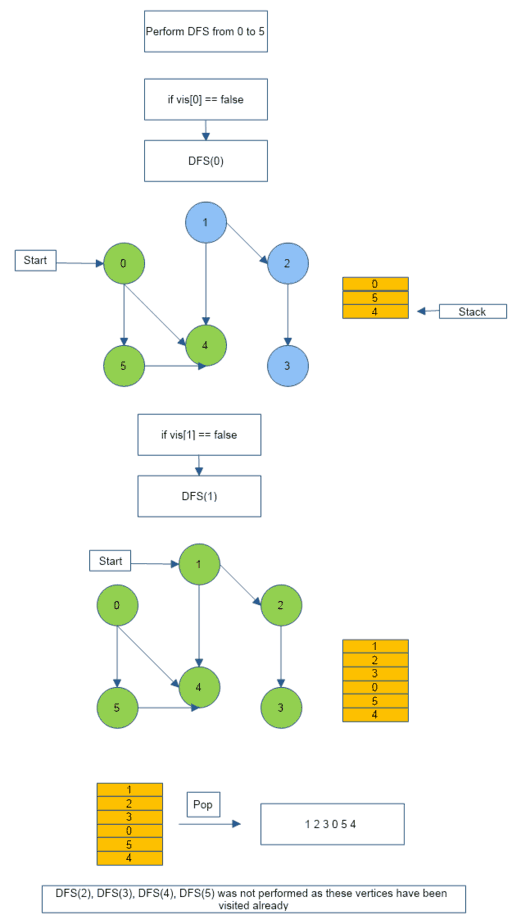
Topological Sorting Example

Topological sorting of above graph is -> {1,2,3,0,5,4}

Theory

• Topological Sorting is done for a Directed Acyclic Graph (DAG).
• A DAG has no cycles in it. ie, there is no such path starting from any node of the graph that comes back to that node.

Topological Sorting Algorithm

1. We perform Depth First Search (DFS) for an unvisited node (source node) and visit all it’s neighbors recursively in a depth-first manner.
2. We mark each neighbor encountered in the path as visited.
3. Once we reach the last node (the node from which has no unvisited neighbor), we backtrack, push each node encountered in the path while backtracking into a stack.
4. The first node pushed into the stack is the last node visited in DFS traversal.
5. The last node pushed into the stack is the first node visited during traversal.

Functions used

• DFS() – perform DFS traversal from a source node.
• topSort() – perform DFS traversal for every unvisited node.

C++ Program

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// add edge in a directed graph
void add(vector <int> list[],int u,int v)
{
    adj[u].push_back(v);
}

// perfrom DFS from source node s
void DFS(int s,vector <int> list[],bool *vis,stack <int> &st)
{
    vis[s] = true;
    for(auto i : list[s])
    {
        // visit a node only if unvisited
        if(!vis[i])
        DFS(i,list,vis,st);
    }

    // push node into stack while backtracking
    st.push(s);
}

void topSort(vector <int> list[],int n)
{
    bool *vis = new vis[n];
    stack <int> st;

    // before performing DFS, mark every node as not visited
    for(int i=0;i<n;i++)
    vis[i] = false;

    // perfrom DFS from every unvisited node
    for(int s=0;s<n;s++)
    if(!vis[s])
    DFS(s,list,vis,st);

    // pop the content of the stack
    // the order of the elements is order in which tasks are to be performed
    while(!st.empty())
    {
        cout<<st.top()<<" ";
        st.pop();
    }
}

int main()
{
    int n = 6;
    vector <int> list[n];

    add(list, 0, 5); 
    add(list, 0, 4); 
    add(list, 5, 4); 
    add(list, 1, 4); 
    add(list, 1, 2); 
    add(list, 2, 3); 
  
    cout <<"Topologically Sorted Graph : ";
    topSort(list,n)
    return 0;
}

Output

Topologically Sorted Graph : 1 2 3 0 5 4

Java Program

import java.io.*;  
import java.util.*;  

class graph
{
    private int v;
    private ArrayList<ArrayList<Integer>> adj;

    // constructor to generate adjacency list
    graph(int n)
    {
        v = n;
        adj = new ArrayList<ArrayList<Integer>> (v);

        for(int i=0;i<v;i++)
        {
            adj.add(new ArrayList<Integer>());
        }
    }

    // add edge in a directed graph
    void add(int u,int v)
    {
        adj.get(u).add(v);
    }

    // perfrom DFS from source node s
    void DFS(int s,boolean vis[],Stack <Integer> st)
    {
        vis[s] = true;
        Integer i;

        Iterator <Integer> itr = adj.get(s).iterator();
        while(itr.hasNext())
        {
            i = itr.next();
             // visit a node only if unvisited
            if(vis[i] == false)
                DFS(i,vis,st);
        }
        // push node into stack while backtracking
        st.push(s);
    }
    

    void topSort()
    {
        Stack <Integer> st = new Stack<Integer>();
        boolean vis[] = new boolean[v];

        // before performing DFS, mark every node as not visited
        for(int i=0;i<v;i++)
        vis[i] = false;

        // perfrom DFS from every unvisited node
        for (int i = 0; i < v; i++)  
        {
             if (vis[i] == false)  
                DFS(i, vis, st);  
        }
        
        // pop the contents of the stack
        // the order of the elements is order in which tasks are to be performed
        while (st.empty() == false)  
            System.out.print(st.pop() + " ");  
    }

    public static void main(String args[]) 
    {
        int n = 6;
        graph g = new graph(n);  
        
        g.add(0, 5);  
        g.add(0, 4);  
        g.add(5, 4);  
        g.add(1, 4);  
        g.add(1, 2);  
        g.add(2, 3);  
    
        System.out.println("Topologically Sorted Graph :");  
        g.topSort();      
    }
}

Output

Topologically Sorted Graph : 1 2 3 0 5 4

Complexity Analysis

• Time Complexity: T(n) = O(V+E)
• Space Complexity: A(n) = O(V), stack used for storing vertices

Supplementary Information

• Topological Sorting is applied in job scheduling in computer science, a set of jobs which are interdependent can be put in a certain order for them to be executed.
• In the above example if each node is a job (having the same numbering as the node), then Job 0 and Job 1 are executed before the execution of Job 4.

Reference  Interview Questions