Given a string s of length n. Check whether there is a closing parenthesis for every opening parentheses i.e. if all the parentheses are balanced. In other words, we can also say that, if we have a ‘}’, ‘)’ and ‘]’ for every ‘{‘, ‘(‘ and ‘[‘ respectively, the expression is said to be balanced.
For instance –
The expression “{ [ ( ) ] }” contains balanced parentheses because it has some kind of closing parenthesis for an opening parenthesis.
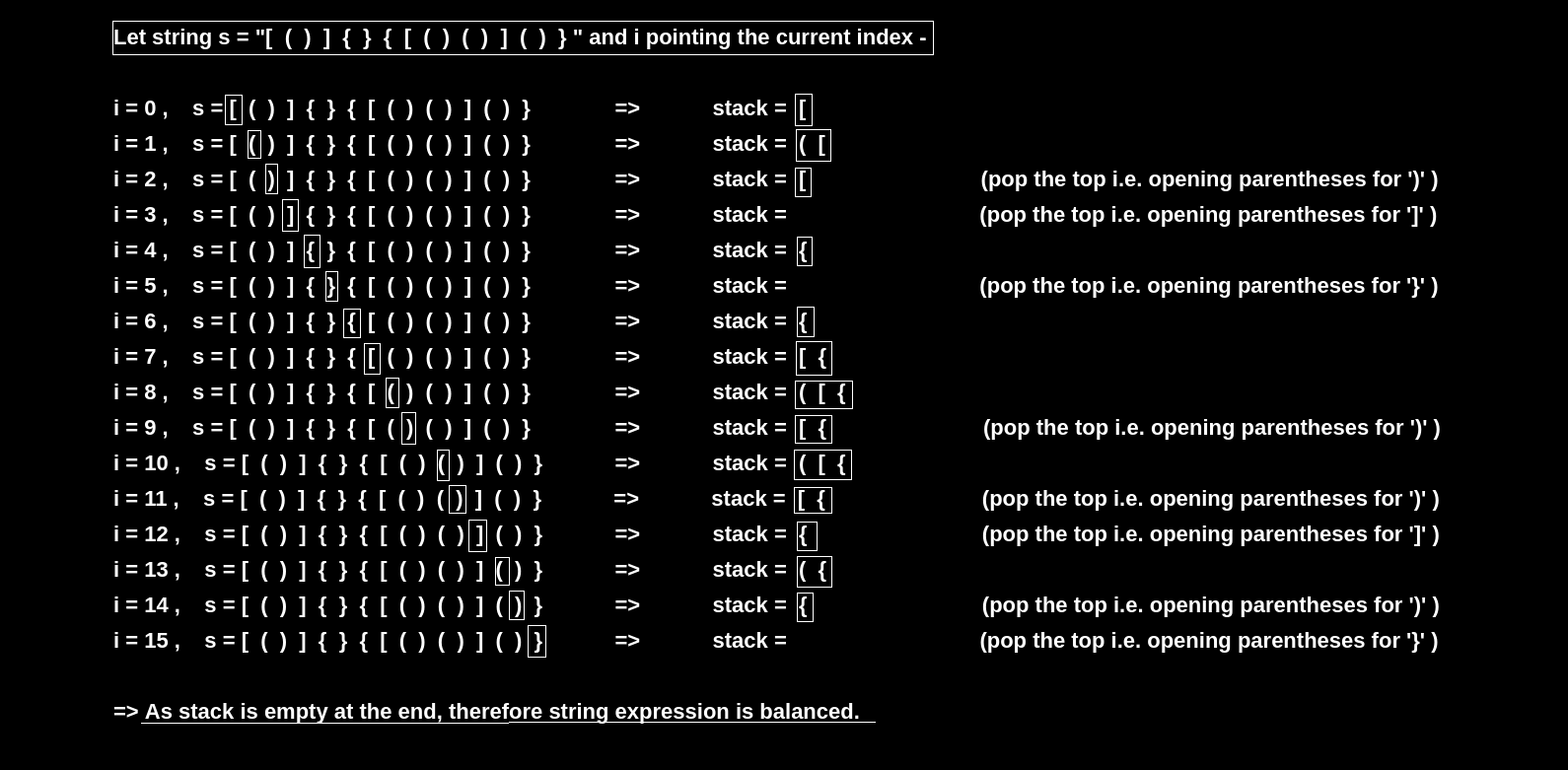
Table of Contents
Example
Input: s = “[()]{}{[()()]()}”
Output: Expression is balanced.
Input: s = “[(){}”
Output: Expression is not balanced.
Method
First, we create a stack. For each character check if it is an opening parenthesis i.e. either ‘{‘, ‘(‘ or ‘[‘, push the character in the stack. Else if it is a closing parenthesis i.e. either ‘}’, ‘)’ or ‘]’, check if the top of the stack is opening parentheses of similar kind pop it from the stack and continue the loop for next characters. Else return false. If Stack is empty at the end it means the expression contains balanced parentheses else the parentheses are unbalanced.
Algorithm
- Initialize a string s of length n.
- Create a stack to store the characters.
- Traverse through the string and check if the current character is an opening parenthesis push it in the stack and continue.
- If the stack is empty return false.
- Switch the closing parenthesis and check if the character at top of stack is the opening parenthesis is of the same type as closing parenthesis pop the top character and break. Else return false.
- If the stack is empty return true, else return false.
C++ Program to check for balanced parentheses in an expression
#include<bits/stdc++.h>
using namespace std;
bool isBalanced(string str){
stack<char> s;
char x;
for(int i=0; i<str.length(); i++){
if(str[i]=='('||str[i]=='['||str[i]=='{'){
s.push(str[i]);
continue;
}
if(s.empty())
return false;
switch(str[i]){
case ')':
x = s.top();
s.pop();
if(x=='{' || x=='[')
return false;
break;
case '}':
x = s.top();
s.pop();
if(x=='(' || x=='[')
return false;
break;
case ']':
x = s.top();
s.pop();
if(x =='(' || x == '{')
return false;
break;
}
}
return (s.empty());
}
int main(){
string s = "[()]{}{[()()]()}";
if(isBalanced(s)){
cout<<"Expression is balanced.";
}
else{
cout<<"Expression is not balanced.";
}
return 0;
}Expression is balanced.
Java Program to check for balanced parentheses in an expression
class Parantheses{
static class stack{
int top=-1;
char items[] = new char[100];
void push(char x){
if(top == 99){
System.out.println("Stack full");
}
else{
items[++top] = x;
}
}
char pop(){
if(top == -1){
System.out.println("Underflow error");
return '\0';
}
else{
char element = items[top];
top--;
return element;
}
}
boolean isEmpty(){
return (top == -1) ? true : false;
}
}
static boolean isPair(char character1, char character2){
if(character1 == '(' && character2 == ')')
return true;
else if(character1 == '{' && character2 == '}')
return true;
else if(character1 == '[' && character2 == ']')
return true;
else
return false;
}
static boolean isBalanced(char s[]){
stack st=new stack();
for(int i=0;i<s.length;i++){
if(s[i] == '{' || s[i] == '(' || s[i] == '[')
st.push(s[i]);
if(s[i] == '}' || s[i] == ')' || s[i] == ']'){
if (st.isEmpty()){
return false;
}
else if( !isPair(st.pop(), s[i])){
return false;
}
}
}
if(st.isEmpty())
return true;
else
return false;
}
public static void main(String[] args){
char s[] = {'[','(',')',']','{','}','{','[','(',')','(',')',']','(',')','}'};
if(isBalanced(s)){
System.out.println("Expression is balanced.");
}
else{
System.out.println("Expression is not balanced.");
}
}
}Expression is balanced.
Complexity Analysis for balanced parentheses in an expression
Time Complexity: O(n) where n is the number of parentheses/characters in the given string.
Auxiliary Space: O(n) where n is the number of parentheses/characters in the given string because here we used space to store n characters in the stack.