Sort a stack using recursion

Difficulty Level Easy
Frequently asked in Amazon Goldman Sachs IBM Kuliza Yahoo
Recursion StackViews 3115

Problem Statement

The problem “Sort a stack using recursion” states that you are given a stack data structure. Sort its elements using recursion. Only the below-listed functions of the stack can be used –

  • push(element) – to insert the element in the stack.
  • pop() – pop() – to remove/delete the element at the top of the given stack.
  • isEmpty() – to check if there is any element in the stack or not.
  • top() – to peek/see the element at the top of the given stack.

Sort a stack using recursion

Example

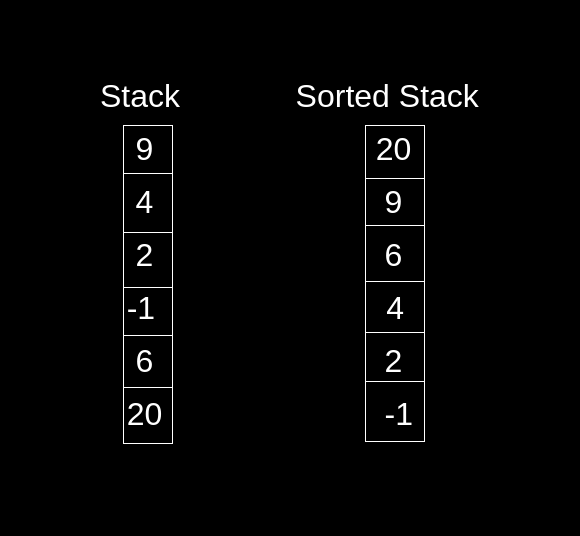
9 4 2 -1 6 20
20 9 6 4 2 -1

Explanation: Since the stack is sorted in ascending order. The maximum element comes at the top. Because stack is LIFO data structure, the output seems to be in descending order.

2 1 4 3 6 5
6 5 4 3 2 1

Algorithm

  1. Initialize a stack and push elements in it.
  2. Create a function to insert the elements in sorted order in the stack which accepts a stack and an element as a parameter. Check if the stack is empty or the given element is greater than the element at the top of the stack, push the element in the stack and return.
  3. Create a temporary variable and store the top of the stack in it. Pop the element at the top of the stack and make the recursive call to the function itself. Push the temporary variable in the stack.
  4. Similarly, create a function sort() that accepts a stack as a parameter. Check if the stack is not empty, create a variable x, and store the top of the stack in it. Pop the element at the top of the stack. Make a recursive call to the function itself. Call the function to insert the elements in sorted order in the stack.
  5. Call the sort function in the main().
  6. Create a function to print the sorted stack which accepts a stack as the parameter. Traverse while the stack is not empty, print the data of the stack and move to the next element.

Code

C++ Program to sort a stack using recursion

#include <iostream> 
using namespace std; 
  
struct stack{  
    int data;  
    struct stack *next;  
};  
  
void initStack(struct stack **s){  
    *s = NULL;  
}  
  
int isEmpty(struct stack *s){  
    if(s == NULL){  
        return 1;  
    }    
    return 0;  
}  
  
void push(struct stack **s, int x){
    
    struct stack *p = (struct stack *)malloc(sizeof(*p));  
  
    if(p == NULL){  
        return;  
    }  
  
    p->data = x;  
    p->next = *s;  
    *s = p;  
}  
  
int pop(struct stack **s){  
    int x;  
    struct stack *temp;  
  
    x = (*s)->data;  
    temp = *s;  
    (*s) = (*s)->next;  
    free(temp);  
  
    return x;  
}  
  
int top(struct stack *s){  
    return (s->data);  
}  
  
void InsertWithSort(struct stack **s, int x){  
    
    if(isEmpty(*s) or x > top(*s)){  
        push(s, x);  
        return;  
    }  
  
    int temp = pop(s);  
    InsertWithSort(s, x);  
  
    push(s, temp);  
}  
  
void sort(struct stack **s){  
    
    if(!isEmpty(*s)){  
        int x = pop(s);  
  
        sort(s);  
  
        InsertWithSort(s, x);  
    }  
}  
  
void print(struct stack *s){  
    while(s){  
        cout<<s->data<<" "; 
        s = s->next;  
    }  
}  
  
int main(){  
    struct stack *top;  
  
    initStack(&top);
    
    push(&top, 9);  
    push(&top, 4);  
    push(&top, 2);  
    push(&top, -1);  
    push(&top, 6);
    push(&top, 20);
  
    sort(&top);  
    
    print(top);  
  
    return 0;  
}
20 9 6 4 2 -1

Java Program to sort a stack using recursion

import java.util.ListIterator; 
import java.util.Stack; 
  
class SortStack{ 
    
    static void InsertWithSort(Stack<Integer> s, int x){ 
        if (s.isEmpty() || x > s.peek()){ 
            s.push(x); 
            return; 
        } 
       
        int temp = s.pop(); 
        InsertWithSort(s, x); 
       
        s.push(temp); 
    } 
       
    static void sort(Stack<Integer> s){ 
        if(!s.isEmpty()){ 
            int x = s.pop(); 
       
            sort(s); 
       
            InsertWithSort(s, x); 
        } 
    } 
      
    static void print(Stack<Integer> s){ 
       ListIterator<Integer> lt = s.listIterator(); 
         
        while(lt.hasNext()){ 
            lt.next(); 
        }       
         
        while(lt.hasPrevious()){ 
           System.out.print(lt.previous()+" ");
        }   
    } 
    
    public static void main(String[] args){
        Stack<Integer> s = new Stack<>(); 
        
        s.push(9);  
        s.push(4);  
        s.push(2);  
        s.push(-1);  
        s.push(6);
        s.push(20); 
       
        sort(s); 
       
        print(s); 
       
    } 
}
20 9 6 4 2 -1

Complexity Analysis

Time Complexity

O(N^2) where n is the number of elements in the stack. Because when we push the element in the stack we may end up removing all the elements which are currently present in the stack and then insert it. This case occurs if the input is in decreasing order.

Space Complexity

O(N) because we used stack space for n elements. While removing elements to place our current element. We had to store the removed elements, which gives us a linear space complexity.

Translate »