binary search tree - binary search tree data structure

A binary search tree is a Binary tree with some rules that allows us to maintain the data in a sorted fashion.

As it is a binary tree hence, a node can have at max 2 children.

Table of Contents

Structure of a Binary Search Tree node

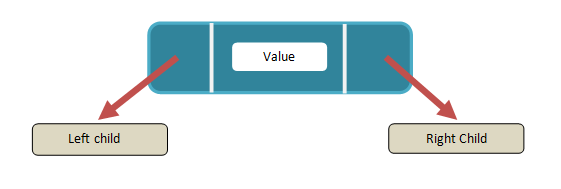
Rules for Binary tree to be a Binary search tree

The nodes present in the left subtree of a node should be less than that node.
The nodes present in the right subtree of a node should be greater than that node.
The above two conditions should be true for all nodes in the tree.

Example

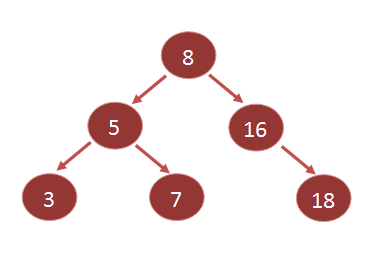
Left subtree of 8 contains: 5, 3, 7 which are smaller than 8

Right subtree of 8 contains: 16, 18 which are greater than 8

Left subtree of 5 contains: 3 which is smaller than 5

Right subtree of 5 contains: 7 which is greater than 5

Left subtree of 16 does not contain any node.

Right subtree of 16 contains: 18 which is greater than 16

3, 7, 18 are leaf nodes hence there will be no left and right subtree present.

Always remember to check the BST conditions for every node.

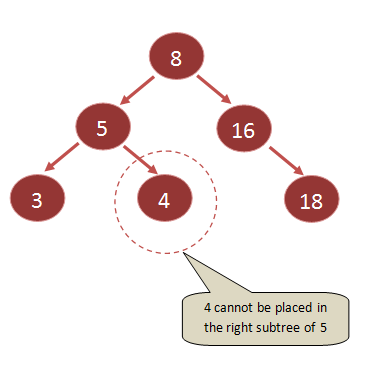
For example:

This is not a Binary Search Tree.

Advantages of Binary Search Tree

Searching can be done in O(log(h)) where h is the height of BST as we can apply binary search on it using the property that the data is stored in a sorted manner in a BST.
Insertion of data in sorted fashion is also done in O(log(h)), whereas other data structures like arrays and linked list this operation will take O(n) time.

Creation of Binary Search Tree

Algorithm

Create a node with the value to be inserted
insertBST(node,value)
1. If root == NULL then return the created node
2. if root->value < key:
  - Insert the created node in the right subtree
  - root->right = insertBST(root->right,value)
3. If root->value > key:
  - Insert the created node in the left subtree
  - root->left = insertBST(root->left,value)

Return root

Let’s understand it with an example:

Consider an array of integer [4, 7, 2, 8, 5]

Let’s create a BST by taking each element from the array sequentially

Step 1: Insert 4

As the root is null, hence make the newly created node as root.

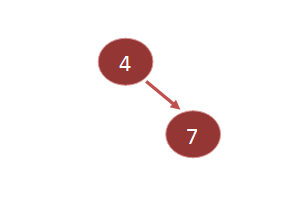
Step 2: Insert 7

Root value is 4, hence 7 should be in the right of root.

Step 3: Insert 2

Root value is 4, hence 2 should be placed in the left of root.

Step 4: Insert 8

Root value is 4, hence 8 should be placed in the right of root.

Now we will check with 7, as 7<8 hence 8 should be placed in the right of 7.

Step 5: Insert 5

Root value is 4, hence 5 should be placed in the right of root.

Now we will check with 7, as 7>5 hence 5 should be placed in the left of 7.

Implementation of Binary Search Tree

C++ Program

#include<bits/stdc++.h>
using namespace std;

struct node
{
    int value;
    struct node* left;
    struct node* right;
    node(int value){             // constructor
        this->value = value;
        this->left = NULL;
        this->right = NULL;
    }
};
struct node* insertBST(node* root, int value)
{
    if (root == NULL) 
        return new node(value);                       // return newly created node

    if (value < root->value)                         // value should be inserted in the left subtree
        root->left  = insertBST(root->left, value);
    else if (value > root->value)                    // value should be inserted in the right subtree
        root->right = insertBST(root->right, value);   
    return root;
}

void inorder(node* root){
    if(root == NULL) 
        return;
    inorder(root->left);
    cout<<root->value<<"-> ";
    inorder(root->right);
}


int main(){
    node *root = NULL;
    root = insertBST(root, 10);     //make the first created node as root
    insertBST(root, 5);
    insertBST(root, 4);
    insertBST(root, 16);
    insertBST(root, 2);
    insertBST(root, 12);
    insertBST(root, 17);

    inorder(root);
}

JAVA Program

class Node { 
    int value; 
    Node left, right; 
  
    public Node(int v) { //constructor
        value = v; 
        left = null;
        right = null; 
    } 
};
class Main { 
    public static Node insertBST(Node root, int value) { 
        if (root == null) { 
            return new Node(value);                            // return newly created node
        }
        if (value < root.value)                               // value should be inserted in the left subtree
            root.left = insertBST(root.left, value); 
        else if (value > root.value)                         // value should be inserted in the right subtree
            root.right = insertBST(root.right, value); 
        return root; 
    } 
    public static void inorder(Node root) { 
        if (root != null) { 
            inorder(root.left); 
            System.out.print(root.value+"-> "); 
            inorder(root.right); 
        } 
    } 
    public static void main(String[] args) { 
        Node root = null; 
        
        root = insertBST(root, 10); //make the first created node as root 
        insertBST(root, 5); 
        insertBST(root, 4); 
        insertBST(root, 16); 
        insertBST(root, 2); 
        insertBST(root, 12); 
        insertBST(root, 17); 
        
        inorder(root);
    } 
}

2-> 4-> 5-> 10-> 12-> 16-> 17->

Structure of the created tree

References