Check if a given array can represent Preorder Traversal of Binary Search Tree

Difficulty Level Easy
Frequently asked in Adobe Amazon LinkedIn
Binary Search Tree Stack TreeViews 2315

The problem “Check if a given array can represent Preorder Traversal of Binary Search Tree” states that you are given a preorder traversal sequence. Now consider this sequence and find out if this sequence can represent a binary search tree or not? The expected time complexity for the solution is O(1).

Example

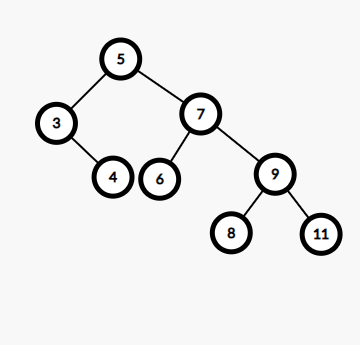
Check if a given array can represent Preorder Traversal of Binary Search Tree

5 3 4 7 6 9 8 11
Yes

Approach to check if preorder sequence represents BST

The problem asks us to check if a given array can represent the Preorder Traversal of the binary search tree. We are given an integer array as input. Now consider that this array has a preorder traversal sequence for the binary search tree. Then check if the given preorder traversal sequence can even represent a binary search tree or not.

A naive approach is to first find out the just greater element than the current element in the right of it. Now check if all the elements in the right of it are greater than the chosen current element. And all the elements in the left of the greater element and the chosen current element are smaller than it. Then recursively check the same condition for the left subarray from the current element to an element less than the just greater element. And also recursively check for the subarray from just greater element to the end. This approach is not efficient because this requires O(N^2) time complexity.

To solve the problem in linear time. We’ll have to find the next greater element using stack. So first create a stack that stores the node values. Then initialize the root as a minimum integer value. Then start with the given input array. If we run over an element that is larger than the stack top. Then keep on removing the elements until the stack is top if greater than the current element or the stack becomes empty. If you come across a node value that is smaller than the root, then the preorder traversal is not correct. In the end when we get past these conditions. We push the current element into the stack.

Code

C++ code to check if a given array can represent preorder traversal of BST

#include<bits/stdc++.h>
using namespace std;

bool preorderBST(int input[], int n)
{
    stack<int> s;
    int root = INT_MIN;
    for(int i=0;i<n;i++)
    {
        // if current node is smaller than the root
        // the current node lies on the right of root
        // thus it is impossible for bst
        if (input[i] < root)
            return false;
        // keep removing elements smaller than the root
        // until you find an element which is greater than the root
        while(!s.empty() && s.top()<input[i])
            root = s.top(), s.pop();
        // if current element is smaller than the root
        // push it into stack
        s.push(input[i]);
    }
    // if we passed until the end of the array
    // that means that the given preorder sequence represents a valid BST
    return true;
}

int main()
{
    int input[] = {5, 3, 4, 7, 6, 9, 8, 11};
    int n = (sizeof input)/(sizeof input[0]);

    cout<<((preorderBST(input, n)) ? "yes" : "no");
}

yes

Java code to check if a given array can represent preorder traversal of BST

import java.util.*;

class Main{
  static boolean preorderBST(int input[], int n)
  {
      Stack<Integer> s = new Stack<Integer>();
      int root = Integer.MIN_VALUE;
      for(int i=0;i<n;i++)
      {
          // if current node is smaller than the root
          // the current node lies on the right of root
          // thus it is impossible for bst
          if (input[i] < root)
              return false;
          // keep removing elements smaller than the root
          // until you find an element which is greater than the root
          while(!s.empty() && s.peek()<input[i]){
              root = s.peek();
              s.pop();
          }
          // if current element is smaller than the root
          // push it into stack
          s.push(input[i]);
      }
      // if we passed until the end of the array
      // that means that the given preorder sequence represents a valid BST
      return true;
  }

  public static void main(String[] args)
  {
      int input[] = {5, 3, 4, 7, 6, 9, 8, 11};
      int n = input.length;

      System.out.print((preorderBST(input, n)) ? "yes" : "no");
  }
}
yes

Complexity Analysis

Time Complexity

O(N), since we have traversed over all the indices in the given input array. Thus the time complexity is linear.

Space Complexity

O(N), because we have used a stack. Thus in the worst-case, we can end up storing all the nodes.

Translate »